定義
 單向連通圖
單向連通圖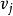 單向連通圖
單向連通圖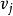 單向連通圖
單向連通圖 單向連通圖
單向連通圖在有向圖中,即使存在從結點 到 的通路,卻未必存在從 到 的通路,即頂點之間的可達關係沒有對稱性。因此,有向圖的連通性分為強連通、 單向連通和 弱連通3種。
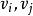 單向連通圖
單向連通圖 單向連通圖
單向連通圖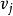 單向連通圖
單向連通圖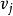 單向連通圖
單向連通圖 單向連通圖
單向連通圖定義1設D是一個有向圖,如果D中任意兩個結點都彼此可達,則稱D為 強連通圖。如果D中任意兩點 之間,有 到 可達或 到 可達(稱為單向可達),則稱D為 單向連通圖。如果有向圖的底圖是無向連通圖,則稱D為 弱連通圖。
注意:強連通圖必是單向連通圖,單向連通圖必是弱連通圖。但反之未必。
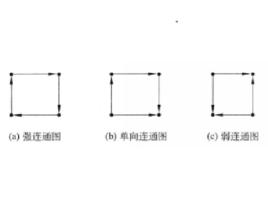
例1 圖1(a)是強連通圖,圖1(b)是單向連通圖,圖1(c)是弱連通圖,圖1(d)不是弱連通圖。
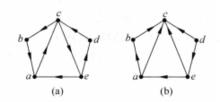 圖1(a)、(b)
圖1(a)、(b)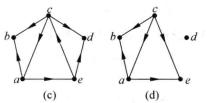 圖1(c)、(d)
圖1(c)、(d) 單向連通圖
單向連通圖定義2設是有向圖,G的極大的單向連通子圖稱為G的 單向連通分 支(unilateral connected component)。
由定義知,如圖2所示有兩個單向連通分支,分別是G[1,2,3,4,5],G[5,6]。
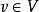 單向連通圖
單向連通圖注意:有向圖G的節點可以位於G的不同的單向連通分支中。
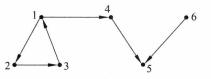 圖2
圖2單向連通圖的判定
關於單向連通圖的判定,有如下定理。
 單向連通圖
單向連通圖 單向連通圖
單向連通圖 單向連通圖
單向連通圖設 是有向圖,則 單向連通若且唯若 中存在一條路,它通過所有節點。
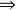 單向連通圖
單向連通圖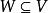 單向連通圖
單向連通圖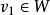 單向連通圖
單向連通圖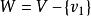 單向連通圖
單向連通圖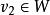 單向連通圖
單向連通圖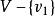 單向連通圖
單向連通圖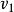 單向連通圖
單向連通圖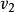 單向連通圖
單向連通圖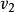 單向連通圖
單向連通圖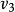 單向連通圖
單向連通圖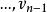 單向連通圖
單向連通圖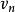 單向連通圖
單向連通圖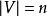 單向連通圖
單向連通圖證法一: ( )若能證明命題“對於任意 均存在一個W中節點在G中到W中其餘節點都有路”,則定理結論成立,因為先取W=V,存在 到其餘V中節點有路,再取 ,存在 到其餘 節點有路.這樣一直下去,就可以得到一條從 到 , 到 , 到 的一條路,其中 (但這條路不一定是軌跡)。
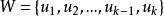 單向連通圖
單向連通圖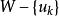 單向連通圖
單向連通圖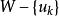 單向連通圖
單向連通圖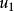 單向連通圖
單向連通圖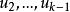 單向連通圖
單向連通圖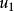 單向連通圖
單向連通圖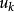 單向連通圖
單向連通圖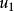 單向連通圖
單向連通圖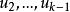 單向連通圖
單向連通圖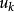 單向連通圖
單向連通圖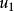 單向連通圖
單向連通圖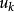 單向連通圖
單向連通圖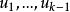 單向連通圖
單向連通圖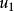 單向連通圖
單向連通圖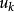 單向連通圖
單向連通圖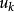 單向連通圖
單向連通圖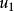 單向連通圖
單向連通圖假定上述命題不成立,令 是使其不成立的元素個數最少的,這時k≥3,根據假設 使命題成立,於是必存在 中一個節點,不妨設為 到其餘節點 有路,而假設 到 是沒有路的,否則與W的假設矛盾。另一方面,由於 到其餘節點 有路,所以 到 沒有路,否則 到 都有路,由於 到 沒有路,而 到 也沒有路,與已知G是單向連通圖矛盾。
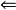 單向連通圖
單向連通圖( )顯然。
證法二:充分性:若G中有一迴路,它至少經過每個頂點一次。則圖中任何兩個頂點都是相互可達的,可見圖G是強連通圖。
必要性:若有向圖G是強連通的,則圖中任何兩個頂點都是相互可達的,故可作出一迴路它經過圖中的所有頂點。否則,必有一迴路不通過某個頂點v,因此v與迴路上的個結點均互不可達,這與G是強連通圖矛盾。
例2 判斷圖3中兩有向圖的連通性。
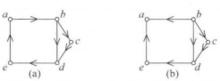 圖3
圖3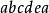 單向連通圖
單向連通圖解:圖3(a)中存在著經過所有點的迴路,故圖3(a)是強連通圖,圖3(b)沒有a到其他頂點的通路,故圖3(b)是單向連通圖。