定義
 連通分量
連通分量 連通分量
連通分量無向圖的極大連通子圖稱為的 連通分量( Connected Component)。任何連通圖的連通分量只有一個,即是其自身,非連通的無向圖有多個連通分量。
相關概念
路徑
 連通分量
連通分量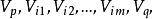 連通分量
連通分量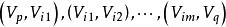 連通分量
連通分量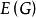 連通分量
連通分量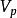 連通分量
連通分量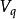 連通分量
連通分量①無向圖的路徑:在無向圖中,若存在一個頂點序列 使得 均屬於 ,則稱頂點 到 存在一條路徑(Path)。
 連通分量
連通分量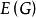 連通分量
連通分量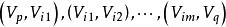 連通分量
連通分量②有向圖的路徑:在有向圖中,路徑也是有向的,它由 中的有向邊 組成。
③路徑長度:路徑長度定義為該路徑上邊的數目。
頂點間的連通性
 連通分量
連通分量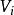 連通分量
連通分量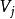 連通分量
連通分量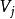 連通分量
連通分量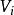 連通分量
連通分量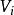 連通分量
連通分量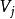 連通分量
連通分量在無向圖中,若從頂點 到頂點 有路徑(當然從 到 也一定有路徑),則稱 和 是連通的。
連通圖
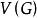 連通分量
連通分量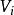 連通分量
連通分量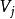 連通分量
連通分量 連通分量
連通分量 連通分量
連通分量若中任意兩個不同的頂點 和 都連通(即有路徑),則稱為連通圖(Connected Graph)。例如,圖是連通圖。
強連通圖
 連通分量
連通分量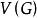 連通分量
連通分量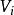 連通分量
連通分量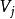 連通分量
連通分量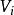 連通分量
連通分量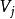 連通分量
連通分量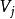 連通分量
連通分量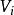 連通分量
連通分量 連通分量
連通分量有向圖中,若對於中任意兩個不同的頂點 和 ,都存在從 到 以及從 到 的路徑,則稱是強連通圖。
強連通分量
 連通分量
連通分量有向圖的極大強連通子圖稱為的強連通分量,強連通圖只有一個強連通分量,即是其自身。非強連通的有向圖有多個強連通分量。
求無向圖的連通分量
作為遍歷圖的套用舉例,下面我們來討論如何求圖的連通分量。無向圖中的極大連通子圖稱為 連通分量。求圖的連通分量的目的,是為了確定從圖中的一個頂點是否能到達圖中的另一個頂點,也就是說,圖中任意兩個頂點之間是否有路徑可達。這個問題從圖上可以直觀地看出答案,然而,一旦把圖存入計算機中,答案就不大清楚了。
對於連通圖,從圖中任一頂點出發遍歷圖,可以訪問到圖的所有頂點,即連通圖中任意兩頂點間都是有路徑可達的。
 連通分量
連通分量 連通分量
連通分量 連通分量
連通分量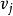 連通分量
連通分量 連通分量
連通分量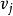 連通分量
連通分量 連通分量
連通分量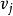 連通分量
連通分量對於非連通圖,從圖中某個頂點 出發遍歷圖,只能訪問到包含頂點 的那個連通分量中的所有頂點,而訪問不到別的連通分量中的頂點。這就是說,在連通分量中的任意一對頂點之間都有路徑,但是如果 和 分別處於圖的不同連通分量之中,則圖中就沒有從 到 的路徑,即從 不可達 。因此,只要求出圖的所有連通分量,就可以知道圖中任意兩頂點之間是否有路徑可達。

