基本概念
知識儲備
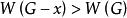 連通度
連通度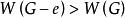 連通度
連通度如果在圖G中刪去一個結點x後,圖G的連通分支數增加,即 ,則稱結點x為G的割點(cut vertex)。如果在圖G中刪去一條邊e後,圖G的連通分支數增加,即 ,則稱e為G的割邊(cut edge)或橋。
沒有割點的非平凡連通圖稱為塊( block)。G中不含割點的極大連通子圖稱為圖G的塊。
若H是圖G的塊,則H自身不含割點且滿足:若向H中再添加邊,但不添加結點,那么H就不是G的子圖了;若向H中再增加結點或邊將H擴大為更大的連通圖,那么H就會含有割點。
例如,圖1所示圖G的塊如圖2所示。
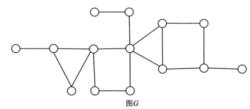 圖1
圖1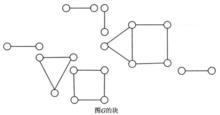 圖2
圖2如果圖G的頂點集的一個真子集T滿足G-T不連通或是平凡圖,則稱T為G的一個 點割( vertex cut)。如果圖G的邊集的一個真子集S滿足G-S不連通或是平凡圖,則稱S為G的一個 邊割(edge cut)。
定義
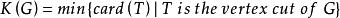 連通度
連通度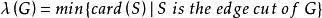 連通度
連通度設G是連通圖,稱 為G的 點連通度( vertex connectivity)或 連通度;稱 為G的 邊連通度(edge conncctivity)。
相關定理
定理1
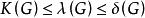 連通度
連通度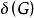 連通度
連通度對一個圖G,有 。其中 是圖G的最小頂點度。
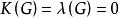 連通度
連通度證明 若G不連通,則 .故上式成立。若G連通,則:
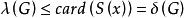 連通度
連通度(1)先證 。
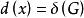 連通度
連通度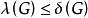 連通度
連通度設x是G中度數最小的頂點,即 ,設所有與x關聯的邊集為S (x),顯然x是圖G-S(x)的一個孤立結點。於是 。
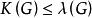 連通度
連通度(2)再證 。
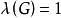 連通度
連通度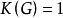 連通度
連通度當 時,顯然有 。
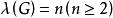 連通度
連通度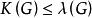 連通度
連通度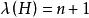 連通度
連通度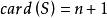 連通度
連通度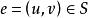 連通度
連通度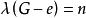 連通度
連通度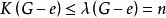 連通度
連通度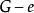 連通度
連通度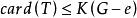 連通度
連通度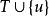 連通度
連通度假設對所有 的圖G,有 。再設 ,S是H的一個邊割,且 。若邊 ,易知 ,故由假設知 ,並設T是 的一個點割,且 。而此時 就是H的一個點割,即
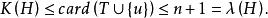 連通度
連通度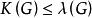 連通度
連通度由歸納法原理知 。證畢。
定理2
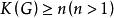 連通度
連通度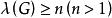 連通度
連通度定義如果無向圖G的連通度 ,則稱圖G是n連通的或G為n連通圖。若 ,則稱圖G是n邊連通的或G為n邊連通圖。
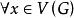 連通度
連通度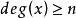 連通度
連通度設圖G是n連通的, ,則 。
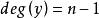 連通度
連通度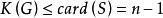 連通度
連通度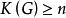 連通度
連通度證明 假設G有一個頂點y且 ,即y與n一1條邊關聯。設與y關聯的n一1個頂點構成的集合為S,顯然S是G的一個點割。因而 。這與 矛盾。
定理3
若G是2邊連通圖,則G有強連通的定向圖。
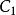 連通度
連通度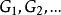 連通度
連通度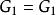 連通度
連通度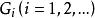 連通度
連通度 連通度
連通度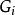 連通度
連通度 連通度
連通度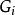 連通度
連通度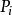 連通度
連通度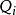 連通度
連通度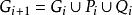 連通度
連通度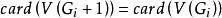 連通度
連通度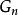 連通度
連通度 連通度
連通度 連通度
連通度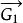 連通度
連通度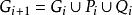 連通度
連通度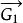 連通度
連通度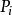 連通度
連通度 連通度
連通度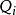 連通度
連通度 連通度
連通度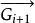 連通度
連通度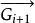 連通度
連通度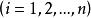 連通度
連通度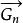 連通度
連通度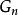 連通度
連通度證明 設G是2邊連通圖,則G必含有圈。先取一個圈 ,歸納地定義G的連通子圖序列 如下: ;若 不是G的生成子圖,設 是在G中而不在 中的一個頂點,則存在從 到 的邊的不重路 和 ,定義 ,由於 ,這個序列必然終止於G的一個生成子圖 。現依次給每個 定向:首先讓 的定向圖 成為一個有向圈;對 ,設已有定向圖 ,讓 成為以 為起點的有向路,而 成為以 為終點的有向路得 ,易見 是強連通有向圖 。因此最後的 是強連通有向圖。由於 是G的生成子圖,所以G有強連通的定向圖。顯然,一個圖G有強連通的定向圖的必要條件是G為2邊連通的。否則G中有割邊,這與G有強連通的定向圖矛盾。證畢。