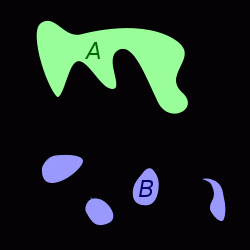
概念
 連通
連通連通單元
拓撲空間的極大連通子集稱作連通單元,每個空間都能表成它的連通單元的不相交聯集。連通單元必然是閉的,在夠好的空間(如流形、代數簇)上也同時是開的,但並非總是如此。例如有理數集上的連通單元都是單元素集合。如果一個空間的連通單元都是單元素集合,則叫做全不連通空間。代數數論中構造的許多拓撲空間都屬於這一類。
道路連通
如果對空間 X 中任兩點 x,y,都存在連續函式 γ:[0,1]→X 使得 γ(0) = x,γ(1) = y,則稱 X 為道路連通空間。若定義中的 γ 可取為使得[0,1]→γ([0,1]) 為同胚,則稱之為弧連通空間。道路連通的豪斯多夫空間必為弧連通空間。
道路連通性保連通性,反之則不然。
局部連通
一個拓撲空間被認為是局部連通的,如果空間中的每一點的任何一個鄰域都包含這個點的一個連通鄰域。這裡所說的連通鄰域,就是指這個鄰域所誘導的子拓撲空間按照上面的定義是一個連通空間。 也可以從拓撲基的角度定義局部連通空間:局部連通空間的拓撲基完全是由連通的集合組成的。