基礎知識
先介紹平面曲線的有關概念。
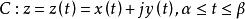 單連通區域
單連通區域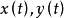 單連通區域
單連通區域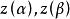 單連通區域
單連通區域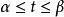 單連通區域
單連通區域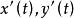 單連通區域
單連通區域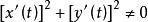 單連通區域
單連通區域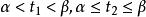 單連通區域
單連通區域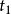 單連通區域
單連通區域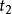 單連通區域
單連通區域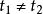 單連通區域
單連通區域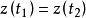 單連通區域
單連通區域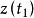 單連通區域
單連通區域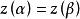 單連通區域
單連通區域定義1 設平面曲線 ,其中 是實的 連續 函式,那么曲線C就稱為 連續曲線, 分別稱為C的 起點與 終點,若在 上, 都連續且對每一個t,有 ,那么曲線C稱為 光滑曲 線。由幾段依次相接的光滑曲線所組成的曲線稱為 逐段光滑曲線。對於滿足 的 與 ,當 且 成立時,點 稱為曲線C的 重點。沒有重點的連續曲線C稱為 簡單曲線或 若爾當(Jardan)曲線。若簡單曲線C的起點與終點重合,即 ,那么曲線C稱為 簡單閉曲線。如圖1所示。
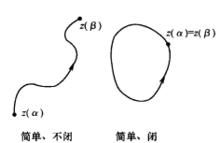 圖1(a)
圖1(a)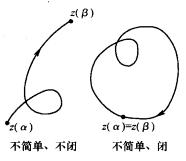 圖1(b)
圖1(b)任意一條簡單閉曲線C把整個複平面唯一地分成三個互不相交的點集,其中除去C以外,一個是有界區域,稱為C的 內部,另一個是無界區域,稱為C的 外部,C為它們的公共邊界,簡單閉曲線的這一性質,其幾何直觀意義是很清楚的。
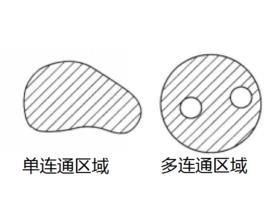
定義2 複平面上的一個區域D,如果在其中任作一條簡單閉曲線,而曲線的內部總屬於D,就稱D為 單連通區域(圖2(a));一個區域如果不是單連通區域,就稱為 多連通區域(圖2(b))。
一條簡單閉曲線的內部是單連通區域(圖2(a)),單連通區域D具有這樣的特徵:屬於D的任何一條簡單閉曲線,在D內可以經過連續的變形而縮成一點,而多連通區域就不具備這個特徵。
 圖2(a)
圖2(a) 圖2(b)
圖2(b)單連通區域的一些性質
 單連通區域
單連通區域 單連通區域
單連通區域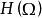 單連通區域
單連通區域我們現在將概述單連通區域的一些性質,這些性質闡明它在全純函式理論中起著重要作用。在這些性質中,(a)和(b)稱為的內拓撲性質;(c)和(d)涉及嵌入s 內的方式;性質(e)到(h)按特徵來說是分析性的;(i)是關於環的代數陳述。
 單連通區域
單連通區域定理1 對於一個平面區域,下面九個條件中的每一個蘊涵著其餘的各個條件:
 單連通區域
單連通區域(a) 同胚於開單位圓盤U;
 單連通區域
單連通區域(b)是單連通的;
 單連通區域
單連通區域 單連通區域
單連通區域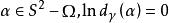 單連通區域
單連通區域(c)對內每一條閉路徑和對每一個;
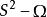 單連通區域
單連通區域(d)是連通的;
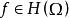 單連通區域
單連通區域 單連通區域
單連通區域(e)每一個能用多項式在的緊子集上一致逼近;
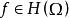 單連通區域
單連通區域 單連通區域
單連通區域 單連通區域
單連通區域(f)對每一個和在內每一條閉路徑,
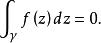 單連通區域
單連通區域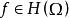 單連通區域
單連通區域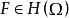 單連通區域
單連通區域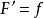 單連通區域
單連通區域(g)每一個對應一個,使得;
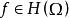 單連通區域
單連通區域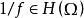 單連通區域
單連通區域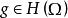 單連通區域
單連通區域(h)如果且,則存在一個,使得
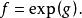 單連通區域
單連通區域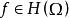 單連通區域
單連通區域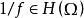 單連通區域
單連通區域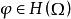 單連通區域
單連通區域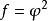 單連通區域
單連通區域(i)如果且,則存在一個,使得。
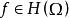 單連通區域
單連通區域 單連通區域
單連通區域 單連通區域
單連通區域 單連通區域
單連通區域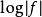 單連通區域
單連通區域 單連通區域
單連通區域定理2 如果,此處為平面內任意開集,且在內沒有零點,則在內調和。
單連通區域內的柯西積分定理
 單連通區域
單連通區域定理3 設在z平面上的單連通區域D內解析,C為D內任意一條圍線,則
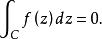 單連通區域
單連通區域 單連通區域
單連通區域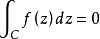 單連通區域
單連通區域推論1 設在單連通區域D內解析,C為D內任意一條閉曲線(C不必為簡單閉曲線),則。
證明: 由於閉曲線C總可以看成區域D內有限條周線銜接而成。因此,由復積分的曲線可加性及定理2即可得結論。
 單連通區域
單連通區域 單連通區域
單連通區域 單連通區域
單連通區域 單連通區域
單連通區域 單連通區域
單連通區域 單連通區域
單連通區域 單連通區域
單連通區域推論2 設函式在單連通區域D內解析,則在D內的積分與路徑無關,即對D內任意兩點以及D內任意兩條以為起點,為終點的路徑和,總有
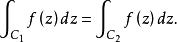 單連通區域
單連通區域