公理簡介
基本的幾何公理之一。指希爾伯特-歐幾里得幾何系統公理表中的第四組公理。它包含2條連續公理:
Ⅳ.(阿基米德公理) 設AB和CD是任意兩條線段,則在直線AB上存在著有限多個點A,A,…,A,使得A在A和A之間,A在A和A之間等,並且線段AA,AA,…,AA都契約於線段CD,而B在A和A之間,如圖1所示。
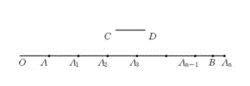 圖1
圖1Ⅳ.(康托爾公理) 設在任意直線a上給了線段的無窮序列AB,AB,…,其中每個後面的都在前面一個的內部;又設不存在這樣的線段,它能在所有這些線段的內部。那么在直線a上,有且僅有一個點x,它落在所有這些線段AB,AB,…的內部。如圖2所示。
 圖2
圖2應當指出,在德國數學家希爾伯特(Hilbert,D.)的經典敘述中,連續公理是由上述阿基米德公理和另一條稱為完備公理的兩條公理組成的,而沒有上述康托爾公理。這裡已對希爾伯特的經典敘述做了改動,亦即把完備公理改成為上述康托爾公理。當然,可以嚴格證明經過改動後的公理系統與原來的公理系統是等價的.所以從本質上說,並沒有作什麼改動。
為便於敘述完備公理,現將經過改動後的希爾伯特-歐幾里得幾何公理系統記為EH,而將在EH中去掉上述康托爾公理後所構成的幾何公理系統記為EH.那么可將希爾伯特經典敘述中的完備公理陳述如下:
對於由被稱為點、直線、平面等幾何元素組成的系統Σ而言,在保有EH的所有公理的情況下,不再允許Σ有任何新的擴充。即不可能再在Σ中引入新的點、直線、平面等幾何元素而構成一個擴張了的系統Σ′,並且在Σ′上保持EH的所有公理。
基本幾何公理
一種重要的幾何公理系統。指德國數學家希爾伯特(D.Hilbert)提出的歐幾里得幾何的公理系統。它包括三個基本元素、三個基本關係和五組(共20條)公理,其基本結構如下表所示:
 圖3
圖3結合公理
亦稱關聯公理或從屬公理。規定基本對象點、直線、平面之間從屬關係的一組公理。基本的幾何公理之一。指希爾伯特-歐幾里得幾何系統公理表中的第一組公理。它包含8條結合公理:
Ⅰ.對於任意兩個不同的點A和B,至少有一直線a連結A和B。
Ⅰ.對於任意兩個不同的點A和B,至多有一直線a連結A和B。
Ⅰ.任一直線上至少存在著兩個點,又至少存在著不在同一條直線上的三個點。
Ⅰ.任給不在同一條直線上的三個點A,B,C,至少存在一個平面通過A,B,C。又任一平面上至少有一個點。
Ⅰ.任給不在同一條直線上的三個點A,B,C,至多存在一個平面通過A,B,C。
Ⅰ.如果一條直線上的兩個點落在同一個平面上,則該直線上的任何一點都落在該平面上。
Ⅰ.如果兩個平面有一個公共點,則它們至少還有另一個公共點。
Ⅰ.至少存在著四個點,它們不在同一個平面上。
應當指出,在上述8條結合公理中,僅有少數幾條出現在《幾何原本》中,大部分是德國數學家希爾伯特(D.Hilbert)補入的。因為歐幾里得(Euclid)和歷史上不少幾何學家在自己的論證中持有空間直覺觀念,例如,他們總是直覺地認為直線上必有無窮多個點,而且既不將此列為公理,又在論證中無條件地承認並使用它。在這個系統里,它可作為一條定理證明之,由於公理應儘可能少,故也不必將此列為公理。
順序公理
基本的幾何公理之一。指希爾伯特-歐幾里得幾何系統公理表中的第二組公理。它包含4條順序公理:
Ⅱ.若A,B,C是直線a的三個不同的點,並且B在A與C之間,則B也在C與A之間。
Ⅱ.任給兩點A和C,則過A和C的直線上至少還存在著一點B,使得C在A和B之間。
Ⅱ.直線上任意三點,至多只有一點在其餘兩點之間。
Ⅱ.德國數學家帕施(Pasch)公理:任給不在同一條直線上的三個點A,B,C,又直線a落在過A,B,C的平面α上,並且a不通過A,B,C中任一點,則當a通過線段AB內部的點時,則a或者還通過線段AC內部的點,或者還通過線段BC內部的點。
契約公理
基本的幾何公理之一。指希爾伯特-歐幾里得幾何系統公理表中的第三組公理。它包含5條契約公理:
Ⅲ.設A,B為直線a上的兩個點,又A′是直線a′(也允許a與a′為同一條直線)上的點,則在a′上點A′的某一側,有且僅有一點B′,使得線段AB與線段A′B′契約(或說AB等於A′B′),記為AB≡A′B′.對於每個線段AB都有契約關係AB≡BA。
Ⅲ.如果線段A′B′和A"B"均契約於線段AB,則A′B′契約於A"B"。
Ⅲ.如果AB和BC是直線a上的兩個線段,且無公共的內部的點,又A′B′和B′C′為同一條或另一條直線a′上的兩個線段,它們也沒有公共的內部的點.如果此時AB≡A′B′且BC≡B′C′,則有AC≡A′C′。
Ⅲ.設∠(h,k)在平面α上,又在同一個或另一個平面α′上給定一直線a′及其確定的一側,h′是由a′上 一點O′出發沿著a′的半直線,那么在a′上由O′出發有且僅有一射線k′,使∠(h,k)契約於∠(h′,k′),同時∠(h′,k′)內部的點都在a′原先確定的一側.如果∠(h,k)契約於∠(h′,k′),則記為∠(h,k)≡∠(h′,k′).又∠(h,k)≡∠(h,k),∠(h,k)≡∠(k,h)。
Ⅲ.設A,B,C為不共線的三個點,而A′,B′,C′亦不在一條直線上.如果AB≡A′B′,AC≡A′C′,並且∠BAC≡∠B′A′C′,則如圖所示,必有∠ABC≡∠A′B′C′,並且∠ACB≡∠A′C′B′。
平行公理
基本的幾何公理之一。指希爾伯特-歐幾里得幾何系統公理表中的第五組公理。其中只含1條平行公理:
Ⅴ.過平面上任一已知直線外的任一點,至多只能引一條直線與該已知直線平行。
注意在歐幾里得幾何意義下,同一平面上沒有公共點的兩條直線稱為平行的。這裡對上述平行公理所採用的敘述方式稱為普萊費爾公理,也是《幾何原本》中之第五公設的等價命題之一。
人物簡介
——希爾伯特
德國著名數學家、哲學家、 數學哲學中形式主義學派的創始人。 1862年生於維拉沃。畢業於克尼格 斯貝爾格大學,後在該校任教授。1893年任哥尼斯堡大學數學教授, 1895年起在哥廷根大學工作達35 年,形成龐大學派,使該大學成為當時世界數學研究中心之一。1913 年當選柏林科學院通訊院士,後成為榮譽院士。1884~1916年主要從事數學研究,幾乎對近代數學的每一個部門,如不變或理論、幾何學原理、積分方程、數學物理學、數學邏輯基礎等均有研究,對相對論和量子理論,也作出了重要貢獻。 1943年在哥廷根逝世。主要著作有 《幾何學基礎》(1899)、《公理化思想》 (1917)、《論無限》(1920)、《數學基礎》 (兩卷,1934、1939,與貝爾奈斯合著)、 《自然認識與邏輯》(1941)等。希爾伯特創立了以建立數學的“形式體系” 為宗旨,以邏輯上的無矛盾性為數 學可靠性和真理性的標準的數學哲學的形式主義,同邏輯主義、直觀主義並稱為數學哲學的三大流派。 在希爾伯特的理論體系中,數學只 是一種抽象的、按一定法則排列的 符號的形式體系,它本身是沒有內 容的,具有無矛盾性。他在哲學問題上有自己獨到的見解: (1)批判 了孔德的不可知論,嘲笑孔德之所 以找不到一個不可解的問題是因為根本就沒有不可解的問題。 (2)在 建立數學理論時,採用了哲學中先 驗的直觀思維方式。先驗的判斷力是構成人類認識活動的基礎,無論 是從事實踐活動還是理論研究工作, 這種判斷力都是必不可少的。以往 所有的哲學問題,歸根到底就是確認有先驗的直觀的思維方式存在, 以此為出發點,進而探討形成每一 個概念知識的可能條件和產生每一 個經驗知識的可能條件。希爾伯特 是20世紀最偉大的數學家之一,他的貢獻深深影響了20世紀的數學發展。
