1,等量加等量仍然是等量;
2,等量減等量仍然是等量;
3,等量乘以等量還是等量;
4,等量除以等量還是等量。
等量公理中非等量原理:
“任何兩個含連續自然數個數相等的區間,篩K次後被篩數(或者未被篩數)相差不超過K個”。
說明:本篩法與埃拉托賽尼篩法不同,埃氏篩先用2篩,然後把2的倍數剔除掉;再用3篩,又把3的倍數剔除掉;再用5篩,.....。本篩法也是按照2,,3,,5...順序篩,用不大於根號n的素數篩。只是已經篩過的數不馬上剔除掉,而是做上標記,等全部篩完過後再把篩過的數剔除掉。於是,有一些含有幾個不同素因子的數就要被篩幾遍,例如“6 ”,就要被“2,”和“3,”各篩一遍。
證明:根據除法算式定理:“給定正整數a和b,b不等於0,存在唯一整數a和r,(0≤r<b.)。使a=bq+r。”得知,如果從a中篩bm形數,a個連續自然數中,最多含有q+1個bm形數,r個連續自然數中,最多含有一個bm形數。例如,a=35,b=3,35=3x11+2,35個連續自然數中,最多含有11+1=12個3m形數,例如1---35有11個3m形數,36----70有12個3m形數。
現在設某兩個區間為A與B,含自然數的個數分別為|A|與|B|,|A|=|B|,下證明p去篩,兩區間被篩pm形數(或者未被篩數)個數相差最多不超過1個。由上所述篩法,用順序素數p1,p2,...,pk依次去篩,兩區間每次被篩pm形數(或者未被篩數)個數相差最多不超過1個,故篩k次兩區間被篩數(或者未被篩數)個數最多不超過k個。
證法1,設|A|=pm+r,則|B|=pm+r,0≤r<p,即區間A和B中均至少含有m(注意m>1)個pm形數,又由於r<p,故r個連續自然數中至多有一個pm形數,即被篩pm形數個數相差不超過1個。
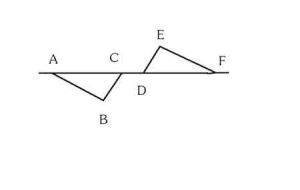
證法2,假若不然,篩k次有兩個區間A與B,被篩數相差大於K,比如有K+1個,那會出現什麼問題呢?我們問第K+1是個什麼(見圖),例如A與B用2和3去篩,如果出現了相差3個,第一個記為2m形,第二個記為3m形,問第三個(-?-)是什麼形式?(每一個括弧表示一個自然數)。
A:(+)。。。(+);-------------------(-)(-)(-)(-)。。。(-);
B:(+)。。。(+)(2m)(3m)(-?-);--------------------(-)。。。(-);
|---------------已經篩過部分----------------|------------未經篩過部分------------|。
如果第三個(-?-)是2m或者3m形, 顯然與除法算式定理矛盾;如果不是2m或者3m形,它就不應該“站在”已經篩過的行列。無論哪一種情況,假設都不能成立。證畢。證明方法2由美國Qhio-Wesleyan-University王蕊珂給出。(如果已經篩過部分A比B多K個,則未篩過部分B比A多k個,這個很好理解,正如一個故事所講,第一輛車裝了40位姑娘,第二輛車裝了40位小伙子,停車時第二輛車的一部分小伙子坐上了第一輛車,第一輛車的司機不高興了,說我只拉40個人,於是兩輛車都是40個人,都有姑娘小伙,問:是第一輛車的姑娘多還是第二輛車的小伙子多?答案是顯然的;第一輛車的姑娘與第二輛車的小伙子一樣多)。
我們可以用公式表示:{|A1|=|A2|=...=|An|}→s(k):|Aj|-|Ai|≤k。
就是說,在連續自然數相等的區間|A1|,|A2|,...,|An|中,篩(用s表示)k 次,任何兩個區間:| Aj|-|Ai|≤k。.
註:原來以為這個問題是顯然的,哪知,論文發表後,江西省九江市第一中學高三級黃晶晶同學發現必須給與證明,否則就是一個漏洞,給編輯部寫信。時間是2002年。 小小年紀,真是不簡單。後來得知,黃晶晶考入一所著名大學的數學系,經過兩年多努力,才完成“任何兩個含連續自然數個數相等的區間,篩k次被篩數(或者未被篩數)相差不大於k個。