克卜勒方程

中文名稱：克卜勒方程 英文名稱：Kepler's equation 定義：表示天體軌道偏心率、平近點角和偏近點角之間關係的一個方程。 套用學科：天文學（一級學科）；天體力學（二級學科）

克卜勒方程

正文

二體問題運動方程的一個積分。它反映天體在其軌道上的位置與時間 t的函式關係。橢圓軌道的克卜勒方程是：

E-esinE=M。

式中 E為偏近點角；e 為軌道偏心率；M 為平近點角；M=n(t-τ)，n為平均角速度，τ為天體過近日點的時刻。這是一個聯繫E和M的超越方程，已證明它的解是存在的並且是唯一的,對於給定的t,可求出M,再用圖解法、數值法或分析法求出E。然後便可以求出天體的極坐標(r,f)。其中r為向徑，f為真近點角。雙曲線軌道的克卜勒方程是：

eshF－F＝v(t－τ)。

式中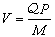，a1為雙曲線軌道的半主徑,μ=G(M+m)，G為萬有引力常數,M+m為兩個天體質量之和；F是雙曲線軌道的輔助量，它與r的關係為r=a1(e ch F－1)。拋物線軌道的克卜勒方程是：

，

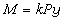q 是軌道近日點距。

配圖

相關連線