簡述
 正n邊形
正n邊形 正n邊形
正n邊形正n邊形指具有n(正整數n≥3)條相等邊的正多邊形,其內角和為 ,每個內角度數為 ,外角和為360°.
對稱性
正n邊形都是軸對稱圖形
當正n邊形的n為偶數時是中心對稱圖形
面積公式
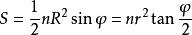 正n邊形
正n邊形(R為正多邊形外接圓半徑,r為正多邊形內切圓半徑,φ為各邊所對圓心角)
尺規作圖
1801年,高斯證明:如果n是質數的費馬數,那么就可以用直尺和圓規作出正n邊形。高斯本人就是根據這個定理作出了正十七邊形,解決了兩千年來懸而未決的難題。

正n邊形,具有n(正整數n≥3)條相等邊的正多邊形,其內角和為180(n-2)°,每個內角度數為180°(n-2)/n,外角和為360°。
 正n邊形
正n邊形 正n邊形
正n邊形正n邊形指具有n(正整數n≥3)條相等邊的正多邊形,其內角和為 ,每個內角度數為 ,外角和為360°.
正n邊形都是軸對稱圖形
當正n邊形的n為偶數時是中心對稱圖形
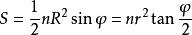 正n邊形
正n邊形(R為正多邊形外接圓半徑,r為正多邊形內切圓半徑,φ為各邊所對圓心角)
1801年,高斯證明:如果n是質數的費馬數,那么就可以用直尺和圓規作出正n邊形。高斯本人就是根據這個定理作出了正十七邊形,解決了兩千年來懸而未決的難題。
正n邊形,具有n(正整數n≥3)條相等邊的正多邊形,其內角和為180(n-2)°,每個內角度數為180°(n-2)/n,外角和為360°。
簡述 對稱性 面積公式 尺規作圖正2^n邊形(n≥2)即正二的n次冪邊形,常見的有正四邊形(正方形)、正八邊形等。任意正2^n均可通過尺規作圖作出。
正十七邊形是指幾何學中有17條邊及17隻角的正多邊形。正十七邊形的每個內角約為158.823529411765°,其內角和為2700°,有119條對角線...
起源 作法 簡易作法正三十邊形是由三十條完全相同的邊和三十個完全相同的角組成的。
正三十六邊形是由三十六條完全相同的邊和三十六個完全相同的角組成的。 正36邊形的每個內角是170°,每個外角是10°。正36邊形既是軸對稱圖形,又是中心...
"邊形.共有三種數可用尺規作圖.(1)
正五十邊形是由50條完全相同的邊和50個完全相同的角組成的;它的每個內角是170°,每個外角是10°。
正十三邊形的簡介 正十三邊形是由十三條完全相同的邊和十三個完全相同的角組成的。
在幾何學中,七邊形是指有七條邊和七個頂點的多邊形,其內角和為900度。七邊形有很多種,其中對稱性最高的是正七邊形。其他的七邊形依照其類角的性質可以分成凸...
簡述 正七邊形 扭歪七邊形 命名 使用