費馬數
費馬費馬數是以數學家費馬命名一組自然數，具有形式：
其中 n 為非負整數。
若 2n + 1 是素數，可以得到 n 必須是2的冪。（若 n = ab，其中 1 < a, b < n 且 b 為奇數，則 2n + 1 ≡ (2a)b + 1 ≡ (−1)b + 1 ≡ 0 (mod 2a + 1)。）也就是說，所有具有形式 2n + 1 的素數必然是費馬數，這些素數稱為費馬素數。已知的費馬素數只有 F0 至 F4 五個。
正文
形如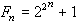
的數，n≥0。前五個費馬數是F0=3,F1=5,F2=17,F3=257,F4=65537,均為素數。據此,1640年，法國數學家P.de費馬猜想Fn均為素數，1732年，L.歐拉發現 F5=641×6700417，故費馬猜想不真。到目前為止，只知道以上五個費馬數是素數。此外，還證明了48個費馬數是複合數。這些複合數可以分成三類：①當n=5,6,7時，得到了Fn的標準分解式；②當n=8,9,10,11,12,13,15,16,18,19,21,23,25,26,27,30,32,36,38,39,42,52,55，58，63,73,77,81,117,125,144,150,207,226,228,250,267,268,284,316,452,556,744,1945時，只知道Fn的部分素因數；③當n=14時，只知道F14是複合數，但是它們的任何真因數都不知道。因此，在費馬數列中是否有無窮多個素數，或者是否有無窮多個複合數，都是未解決的問題。自從費馬猜想被否定後，有人猜想費馬數列中只有有限個素數，這一猜想也未解決。還有一個未能證明的猜想：費馬數無平方因子。L.J.沃倫於1967年證明了：如果素數q滿足q2｜Fn，則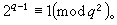
費馬數有一些簡單的性質：如①當整數 k>0時，有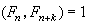
；②設 n>0，Fn 是素數的充分必要條件是
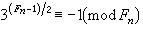；③設 n>1，Fn的每一個素因數形如
。
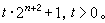1801年,C.F.高斯證明了,當h＝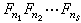
(0≤n1<n2<…<ns,s≥1),Fnt(t=1,2,…,s)都是素數時,正h邊形可用圓規和直尺來作圖，可見費馬數與平面幾何的一些問題有聯繫。近年來，費馬數在數位訊號處理中得到套用。例如，費馬數變換(FNT),即以費馬數給出的數論變換,在數論變換中最為有用。
