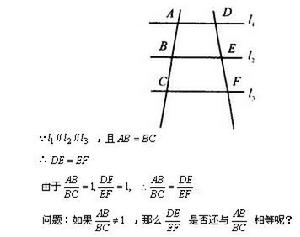
事前機率 :
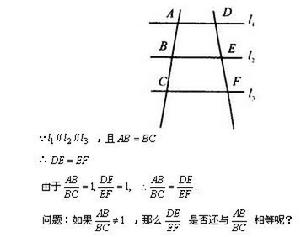 貝氏定理
貝氏定理先了解母體的特性後,再設法求出某一事件出現的機率,此種方法稱為事前機率。
事後機率 :
在實務上常利用事件所呈現的額外資訊去修正事前機率。
概述
兩個事件A和B的發生機率分別為P(A)和P(B),若P(A)為事前機率,且可得知額外資訊P(B|A),依據貝氏定理可求得事後機率P(A|B),其過程如下:
P(A|B)=P(A∩B)/P(B)=P(A).P(B|A)/P(B)
兩事件之貝氏定理
設A、B為任意兩個事件,則
P(A|B)= (P(A).P(B|A))/P(B)
= (P(A).P(B|A))/(P(B|A).P(A)+ P(B|Ac).P(Ac))
貝氏定理
設B1, B2, …, Bn為樣本空間S之一分割,則對任意一事件B,當P(B)≠0,則
P(Aj|B)= (P(Aj).P(B|Aj))/P(B)
= (P(Aj).P(B|Aj))/(ΣP(Ai).P(B|Ai))
, 1≦i≦n
貝氏機率是由貝氏理論所提供的一種對機率的解釋,它採用將機率定義為某人對一個命題信任的程度的概念。貝氏理論同時也建議貝氏定理可以用作根據新的信息導出或者更新現有的置信度的規則。
歷史
貝氏定理和貝氏機率以托馬斯·貝葉斯(1702-1761)命名,他證明了現在稱為貝氏定理的一個特例。術語貝葉斯卻是在1950年左右開始使用,很難說貝葉斯本人是否會支持這個以他命名的機率非常廣義的解釋。拉普拉斯證明了貝氏定理的一個更普遍的版本,並將之用於解決天體力學、醫學統計中的問題,在有些情況下,甚至用於法理學。但是拉普拉斯並不認為該定理對於機率論很重要。他還是堅持使用了機率的經典解釋。Frank P. Ramsey在《數學基礎》(1931年)中首次建議將主觀置信度作為機率的一種解釋。Ramsey視這種解釋為機率的頻率解釋的一個補充,而頻率解釋在當時更為廣泛接受。統計學家Bruno de Finetti於1937年採納了Ramsey的觀點,將之作為機率的頻率解釋的一種可能的代替。L. J. Savage在《統計學基礎》(1954年)中拓展了這個思想。有人試圖將“置信度”的直觀概念進行形式化的定義和套用。最普通的套用是基於打賭:置信度反映在行為主體願意在命題上下注的意願上。當信任有程度的時候,機率計算的定理測量信任的理性程度,就像一階邏輯的定理測量信任的理性程度一樣。很多人將置信度視為經典的真值(真或假)的一種擴展。Harold Jeffreys, Richard T. Cox, Edwin Jaynes和I. J. Good研探了貝氏定理。其他著名貝氏定理的支持者包括[[John Maynard Keynes和B.O. Koopman]]。
套用
自1950年代以來,貝氏定理和貝氏機率通過考克斯定理, Jaynes的最大熵原理以及荷蘭書論證得到了廣泛的套用。在很多套用中,貝氏方法更為普適,也似乎較頻率機率能得出更好的結果。貝氏因子也和奧卡姆剃刀一起使用。數學套用請參看貝氏推論和貝氏定理。有些人將貝氏推論視為科學方法的一種套用,因為通過貝氏推論來更新機率要求從對於不同假設的初始信任度出發,採集新的信息(例如通過做試驗),然後根據新的信息調整原有的信念。調整原有的信念可以意味著(更加接近)接受或者推翻初始的假設。貝氏技術最近被套用於垃圾郵件的過濾上。貝氏垃圾郵件過濾器採用電子郵件的一個參考集合來定義什麼最初被認為是垃圾郵件。定義了參考之後,過濾器使用參考中的特點來將新的郵件判定為垃圾郵件或有效郵件。新電子郵件作為新的信息出現,並且如果用戶在垃圾郵件和有效郵件的判定中發現錯誤,這個新的信息會更新初始參考集合中的信息,以期將來的判定可以更為精確。
舉例分析
可以將貝葉斯法則的分析思路表達如下。
 貝氏定理
貝氏定理挑戰者B不知道原壟斷者A是屬於高阻撓成本類型還是低阻撓成本類型,但B知道,如果A屬於高阻撓成本類型,B進入市場時A進行阻撓的機率是20%(此時A為了保持壟斷帶來的高利潤,不計成本地拚命阻撓);如果A屬於低阻撓成本類型,B進入市場時A進行阻撓的機率是100%。
博弈開始時,B認為A屬於高阻撓成本企業的機率為70%,因此,B估計自己在進入市場時,受到A阻撓的機率為:
0.7×0.2+0.3×1=0.44
0.44是在B給定A所屬類型的先驗機率下,A可能採取阻撓行為的機率。
當B進入市場時,A確實進行阻撓。使用貝葉斯法則,根據阻撓這一可以觀察到的行為,B認為A屬於高阻撓成本企業的機率變成A屬於高成本企業的機率=0.7(A屬於高成本企業的先驗機率)×0.2(高成本企業對新進入市場的企業進行阻撓的機率)÷0.44=0.32
根據這一新的機率,B估計自己在進入市場時,受到A阻撓的機率為:
0.32×0.2+0.68×1=0.744
 貝氏定理
貝氏定理如果B再一次進入市場時,A又進行了阻撓。使用貝葉斯法則,根據再次阻撓這一可觀察到的行為,B認為A屬於高阻撓成本企業的機率變成 A屬於高成本企業的機率=0.32(A屬於高成本企業的先驗機率)×0.2(高成本企業對新進入市場的企業進行阻撓的機率)÷0.744=0.086 這樣,根據A一次又一次的阻撓行為,B對A所屬類型的判斷逐步發生變化,越來越傾向於將A判斷為低阻撓成本企業了。 以上例子表明,在不完全信息動態博弈中,參與人所採取的行為具有傳遞信息的作用。儘管A企業有可能是高成本企業,但A企業連續進行的市場進入阻撓,給B企業以A企業是低阻撓成本企業的印象,從而使得B企業停止了進入地市場的行動。 應該指出的是,傳遞信息的行為是需要成本的。假如這種行為沒有成本,誰都可以效仿,那么,這種行為就達不到傳遞信息的目的。只有在行為需要相當大的成本,因而別人不敢輕易效仿時,這種行為才能起到傳遞信息的作用。 傳遞信息所支付的成本是由信息的不完全性造成的。但不能因此就說不完全信息就一定是壞事。研究表明,在重複次數有限的囚徒困境博弈中,不完全信息可以導致博弈雙方的合作。理由是:當信息不完全時,參與人為了獲得合作帶來的長期利益,不願過早暴露自己的本性。這就是說,在一種長期的關係中,一個人乾好事還是幹壞事,常常不取決於他的本性是好是壞,而在很大程度上取決於其他人在多大程度上認為他是好人。如果其他人不知道自己的真實面目,一個壞人也會為了掩蓋自己而在相當長的時期內做好事。
貝氏機率的變種
術語主觀機率, 個人機率, 認知機率和邏輯機率描述了通常成為貝氏學派的思想中的一些。這些概念互相重疊,但有不同的側重。這裡提到的一些人物不會自稱是貝氏學派的。貝氏機率應該測量某一個體對於一個不確定命題的置信程度,因此在這個意義下是主觀的。有些自稱貝氏學派的人並不接受這種主觀性。客觀主義學派的主要代表是Edwin Thompson Jaynes和Harold Jeffreys。也許現在還在世的主要客觀貝氏學派人物是杜克大學的James Berger。Jose Bernardo和其他一些人接受一定程度的主觀性,但相信在很多實際情況中有使用"先驗參照(reference priors)"的需要。邏輯(或者說,客觀認知)機率的推崇者,例如Harold Jeffreys, Rudolf Carnap, Richard Threlkeld Cox和Edwin Jaynes, 希望將能夠在兩個有相同關於某個不確定命題的真實性相關的信息的人計算出同樣的機率的技術規律化。這種機率不和個人相關,而只和認知情況相關,因此位於主觀和客觀之間。但是,他們推薦的方法有爭議。批評者對這個聲稱發起挑戰,在關於相關事實的信息缺乏的時候,更偏好某一個置信度是有現實依據的。另一個問題是迄今為止的技術對於處理實際問題還是不夠的。
貝氏機率和頻率機率
貝氏機率和頻率機率相對,它從確定的分布中觀測到的頻率或者在樣本空間中的比例來導出機率。採用頻率機率的統計和機率的理論由R.A. Fisher, Egon Pearson和Jerzy Neyman在20世紀上半葉發展起來。A. N. Kolmogorov也採用頻率機率來通過勒貝格積分為測度論中的機率奠定數學基礎(《機率論基礎》(1933年))。Savage, Koopman, Abraham Wald和其他一些學者自1950年以來發展了貝氏機率。貝氏學派和頻率學派在機率解釋上的分歧在統計學實踐上有重要的結果。例如,在用同樣的數據比較兩個假設的時候,假設測試理論基於機率的頻率解釋,它允許基於錯誤推出數據更支持另外那個模型/假設的機率來否定或接受一個模型/假設(零假設)。出現這種錯誤的機率稱為一類誤差,它要求考慮從同樣的數據源導出的假想的數據集合要比實際觀測到的數據更為極端。這個方法允許論斷'或者兩個假設不同或者觀測到的數據是誤導性的集合'。相對應的是,貝氏方法基於實際觀測到的數據,因此能夠對於任何數量的假設直接賦予後驗機率。對於代表每個假設的模型的參數必須賦予機率的要求是這種直接方法的代價。