置信度
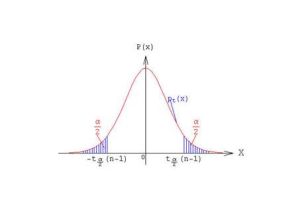
在統計學中，一個機率樣本的置信區間（Confidence interval）是對這個樣本的某個總體參數的區間估計。置信區間展現的是這個參數的真實值有一定機率落在測量結果的周圍的程度。置信區間給出的是被測量參數的測量值的可信程度，即前面所要求的“一定機率”。這個機率被稱為置信水平。
基本信息
- 中文名：置信度
- 英文名：confidence level
- 別稱：可靠度、置信水平、置信係數
- 釋義：個體對待特定命題性相信的程度
簡介
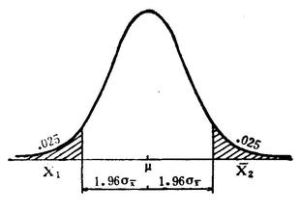置信度在一次大選中某人的支持率為55%，而置信水平0.95上的置信區間是（50%,60%），那么他的真實支持率有百分之九十五的機率落在百分之五十和百分之六十之間，因此他的真實支持率不足一半的可能性小於百分之2.5（假設分布是對稱的）。
如例子中一樣，置信水平一般用百分比表示，因此置信水平0.95上的置信區間也可以表達為：95%置信區間。置信區間的兩端被稱為置信極限。對一個給定情形的估計來說，置信水平越高，所對應的置信區間就會越大。
對置信區間的計算通常要求對估計過程的假設（因此屬於參數統計），比如說假設估計的誤差是成常態分配的。
置信區間只在頻率統計中使用。在貝葉斯統計中的對應概念是可信區間。但是可信區間和置信區間是建立在不同的概念基礎上的，因此一般上說取值不會一樣。置信空間表示通過計算估計值所在的區間。置信水平表示準確值落在這個區間的機率。置信區間表示具體值範圍，置信水平是個機率值。例如：估計某件事件完成會在10~12日之間，但這個估計準確性大約只有80%：表示置信區間（10,12），置信水平80%。要想提高置信水平，就要放寬置信空間。
置信水平是指總體參數值落在樣本統計值某一區內的機率；而置信區間是指在某一置信水平下，樣本統計值與總體參數值間誤差範圍。置信區間越大，置信水平越高。
指標
置信水平Confidencelevel是描述GIS中線元素與面元素的位置不確定性的重要指標之一。置信水平表示區間估計的把握程度，置信區間的跨度是置信水平的正函式，即要求的把握程度越大，勢必得到一個較寬的置信區間，這就相應降低了估計的準確程度。