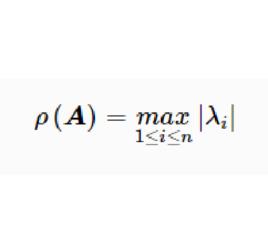定義
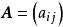 譜半徑
譜半徑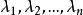 譜半徑
譜半徑若 是複數域上的n階方陣,又 是A的全部特徵值,則
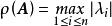 譜半徑
譜半徑稱為 A的譜半徑。
譜半徑的估計
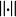 譜半徑
譜半徑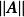 譜半徑
譜半徑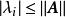 譜半徑
譜半徑在討論矩陣的範數時,我們知道,矩陣 A的每一個特徵值的模(絕對值),都不超過矩陣 A(在任意一種矩陣範數 定義下)的範數 即 。
由此即得:
定理1
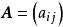 譜半徑
譜半徑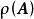 譜半徑
譜半徑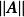 譜半徑
譜半徑複數域上的任一n階方陣 的譜半徑 都不超過 A的範數 即
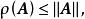 譜半徑
譜半徑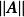 譜半徑
譜半徑這裡 是任一方陣範數。
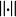 譜半徑
譜半徑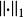 譜半徑
譜半徑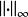 譜半徑
譜半徑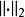 譜半徑
譜半徑若取方陣範數 為 , 或 ,則有下面的推論:
推論
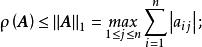 譜半徑
譜半徑(1)
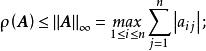 譜半徑
譜半徑(2)
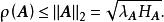 譜半徑
譜半徑(3)
 譜半徑
譜半徑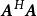 譜半徑
譜半徑這裡 為矩陣 的最大特徵值。
 譜半徑
譜半徑當 是正規矩陣時,則有下述定理。
定理2
若 A為n階正規矩陣,則
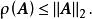 譜半徑
譜半徑證明 因 A是正規矩陣,故存在酉矩陣 P,使得
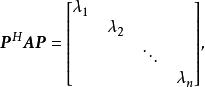 譜半徑
譜半徑由此可得
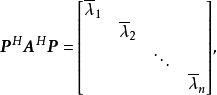 譜半徑
譜半徑從而
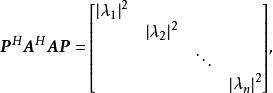 譜半徑
譜半徑又顯然有
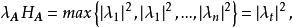 譜半徑
譜半徑 譜半徑
譜半徑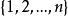 譜半徑
譜半徑這裡是 中的某一值,因此有
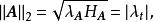 譜半徑
譜半徑而
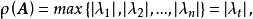 譜半徑
譜半徑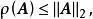 譜半徑
譜半徑所以 證畢。
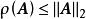 譜半徑
譜半徑由於對角形矩陣、實對稱矩陣、實反對稱矩陣、正交矩陣、酉矩陣、厄米特矩陣、反厄米特矩陣都是正規矩陣,所以對於它們都具有性質 。
定理3
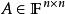 譜半徑
譜半徑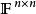 譜半徑
譜半徑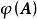 譜半徑
譜半徑 譜半徑
譜半徑對任意 ,存在 上的某種矩陣範數 ,使得對任意 恆有
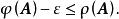 譜半徑
譜半徑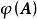 譜半徑
譜半徑注意:這裡的矩陣範數與矩陣 A無關。