定義
由於任何物理運動都需要經過時間的演進才會有實際的位移,所以稱保持時間不變的位移為 虛位移。
 虛位移
虛位移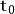 虛位移
虛位移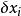 虛位移
虛位移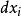 虛位移
虛位移約束隨時間 t改變的力學系統的位置變數在( t 一經指定便為常量)時的虛位移定義為適合 t= t 的約束方程的無限小想像位移。在約束許可情況下所能產生的位移稱為“可能位移”,用表示。對於定常系統,虛位移和可能位移兩者相同,但對非定常系統,兩者則不同。例如,對於含有時間參量的幾何約束
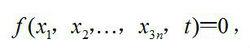 虛位移
虛位移對虛位移有:
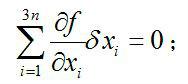 虛位移
虛位移對可能位移有:
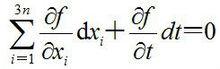 虛位移
虛位移除 f中不含 t;否則上兩式不同。
對於線性運動約束
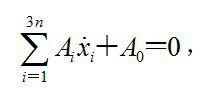 虛位移
虛位移可能位移計算式為:
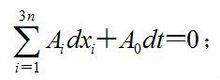 虛位移
虛位移虛位移計算式為:
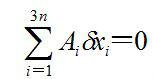 虛位移
虛位移虛位移的套用在於導出虛功原理和動力學普遍方程。
性質
 虛位移
虛位移 虛位移
虛位移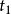 虛位移
虛位移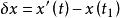 虛位移
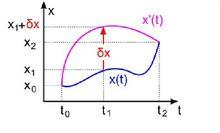
虛位移如右圖,假設一個粒子的運動軌道是,另外一條不違反約束條件的路徑是,則在時間,虛位移是。
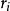 虛位移
虛位移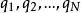 虛位移
虛位移 虛位移
虛位移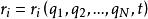 虛位移
虛位移假設一個位置矢量是廣義坐標與時間的函式,,則此位置矢量的無窮小位移為
 虛位移
虛位移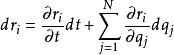 虛位移
虛位移;
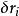 虛位移
虛位移虛位移為
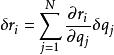 虛位移
虛位移。
 虛位移
虛位移 虛位移
虛位移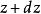 虛位移
虛位移 虛位移
虛位移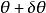 虛位移
虛位移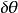 虛位移
虛位移物理系統的運動必須符合設定的約束條件,虛位移也必須符契約束條件。例如,假設一個彈珠被約束地只能移動於一個直立的圓圈。它的位置可以用角坐標表示所在地點的角度。如果彈珠是在圓圈的頂端,將彈珠從高度往上移至高度是一個會違反約束,唯有可能的虛位移是將彈珠從位置移至;這裡,可以是正數或負數。
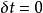 虛位移
虛位移特別注意,虛位移只是空間位移;時間是固定的。雖然某一數值是空間與時間的參數,當計算此數值的虛全微分時,完全不考慮時間的相依性,也就是說。它給出無需力的作用或任何時間過程,是非時間參量的變化引起的,它對質點或質點系的特性,如平衡狀態、運動狀態、能量等等,不會帶來任何影響。
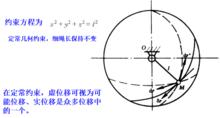 空間單擺定常約束
空間單擺定常約束在定常約束條件下,虛位移和可能位移、實位移的約束方程相同,可以把虛位移視為可能發生卻尚未發生的可能位移,實位移是眾多虛位移中的一個。但對於非定常系統,約束方程的形式不同。在非定常約束,實位移是眾多可能位移中的一個,虛位移不能視為可能位移,實位移也不是眾多虛位移中的一個。
如右圖所示的定長空間單擺,它的虛位移可視為可能位移、實位移,是眾多位移中的一個。
而變長空間單擺的約束,虛位移不能視為可能位移,實位移也不是眾多虛位移中的一個。
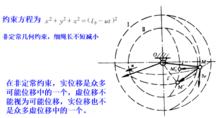 變長空間單擺非定常約束
變長空間單擺非定常約束 虛位移
虛位移套用
分析靜力學的原理。又稱虛功原理。可敘述為受理想、雙面、定常約束的質點系保持平衡的必要和充分條件是所有作用在質點繫上的主動力對其作用點的虛位移所作的虛功之和為零。對n個質點組成的質點系,作用在第i個質點上的主動力Fi與此質點的虛位移的乘積代數和等於0。所謂虛位移是指在一定位置上的質點所作的為約束所允許的、假想的無限小位移。虛位移原理的表達式中不出現未知約束力Ni(因在理想約束作用下,質點系的約束力對其作用點的虛位移所作的功之和為零),因而用它求解靜力學問題極為簡便。若將摩擦力視為主動力,則虛位移原理可套用於非理想約束系統。當質點不脫離約束面時,此原理也可用於單面約束系統。如解除約束並把約束力視為主動力,則此原理還可用來求解約束力。
因此,虛位移原理在確定系統的平衡條件、解決簡單機械的平衡問題、求解結構的約束力等方面有廣泛套用。