簡介
研究多個自變數與因變數相互關係的一組統計理論和方法。又稱多變數分析。多元分析是單變數統計方法的發展和推廣。人的心理和行為具有複雜的內在結構,受到多種因素的制約。僅採用單變數分析難以揭示其內在結構以及各種影響因素的主次作用和互動影響。
首先涉足多元分析方法是F.高爾頓，他於1889年把雙變數的常態分配方法運用於傳統的統計學，創立了相關係數和線性回歸。其後的幾十年中，C.E.斯皮爾曼提出因素分析法（見因素分析），R.A.費希爾提出方差分析和判別分析，S.S.威爾克斯發展了多元方差分析，H.霍特林確定了主成分分析和典型相關。到20世紀前半葉，多元分析理論大多已經確立。60年代以後，隨著計算機科學的發展，多元分析方法在心理學以及其他許多學科的研究中得到了越來越廣泛的套用。
常用的多元分析方法包括3類:①多元方差分析、多元回歸分析和協方差分析，稱為線性模型方法，用以研究確定的自變數與因變數之間的關係；②判別函式分析和聚類分析,用以研究對事物的分類；③主成分分析、典型相關和因素分析，研究如何用較少的綜合因素代替為數較多的原始變數。
多元方差分析
是把總變異按照其來源（或實驗設計）分為多個部分，從而檢驗各個因素對因變數的影響以及各因素間互動作用的統計方法。例如，在分析2×2析因設計資料時，總變異可分為分屬兩個因素的兩個組間變異、兩因素間的互動作用及誤差（即組內變異）等四部分,然後對組間變異和互動作用的顯著性進行F檢驗。
多元方差分析的優點是可以在一次研究中同時檢驗具有多個水平的多個因素各自對因變數的影響以及各因素間的互動作用。其套用的限制條件是，各個因素每一水平的樣本必須是獨立的隨機樣本，其重複觀測的數據服從常態分配，且各總體方差相等。
多元回歸分析
用以評估和分析一個因變數與多個自變數之間線性函式關係的統計方法。一個因變數y與自變數x1、x2、…xm有線性回歸關係是指：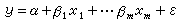
。其中α、β1…βm是待估參數，ε是表示誤差的隨機變數。通過實驗可獲得x1、x2…xm的若干組數據以及對應的y值，利用這些數據和最小二乘法就能對方程中的參數作出估計，記為╋、勮…叧，它們稱為偏回歸係數。
多元回歸分析的優點是可以定量地描述某一現象和某些因素間的線性函式關係。將各變數的已知值代入回歸方程便可求得因變數的估計值（預測值），從而可以有效地預測某種現象的發生和發展。它既可以用於連續變數，也可用於二分變數（0，1回歸）。多元回歸的套用有嚴格的限制。首先要用方差分析法檢驗自變數y與m個自變數之間的線性回歸關係有無顯著性，其次，如果y與m個自變數總的來說有線性關係，也並不意味著所有自變數都與因變數有線性關係，還需對每個自變數的偏回歸係數進行t檢驗,以剔除在方程中不起作用的自變數。也可以用逐步回歸的方法建立回歸方程，逐步選取自變數，從而保證引入方程的自變數都是重要的。
協方差分析
把線性回歸與方差分析結合起來檢驗多個修正均數間有無差別的統計方法。例如，一個實驗包含兩個多元自變數，一個是離散變數(具有多個水平)，一個是連續變數，實驗目的是分析離散變數的各個水平的優劣，此變數是方差變數；而連續變數是由於無法加以控制而進入實驗的，稱為協變數。在運用協方差分析時，可先求出該連續變數與因變數的線性回歸函式，然後根據這個函式扣除該變數的影響，即求出該連續變數取等值情況時因變數的修正均數，最後用方差分析檢驗各修正均數間的差異顯著性，即檢驗離散變數對因變數的影響。
協方差分析兼具方差分析和回歸分析的優點，可以在考慮連續變數影響的條件下檢驗離散變數對因變數的影響，有助於排除非實驗因素的干擾作用。其限制條件是，理論上要求各組資料（樣本）都來自方差相同的正態總體,各組的總體直線回歸係數相等且都不為0。因此套用協方差分析前應先進行方差齊性檢驗和回歸係數的假設檢驗，若符合或經變換後符合上述條件，方可作協方差分析。
判別函式分析
判定個體所屬類別的統計方法。其基本原理是：根據兩個或多個已知類別的樣本觀測資料確定一個或幾個線性判別函式和判別指標，然後用該判別函式依據判別指標來判定另一個個體屬於哪一類。
判別分析不僅用於連續變數，而且藉助於數量化理論亦可用於定性資料。它有助於客觀地確定歸類標準。然而，判別分析僅可用於類別已確定的情況。當類別本身未定時，預用聚類分析先分出類別，然後再進行判別分析。
聚類分析
解決分類問題的一種統計方法。若給定n個觀測對象，每個觀察對象有p個特徵（變數），如何將它們聚成若干可定義的類?若對觀測對象進行聚類,稱為Q型分析;若對變數進行聚類,稱為R型分析。聚類的基本原則是,使同類的內部差別較小,而類別間的差別較大。最常用的聚類方案有兩種。一種是系統聚類方法。例如，要將n個對象分為k類,先將n個對象各自分成一類,共n類。然後計算兩兩之間的某種“距離”，找出距離最近的兩個類、合併為一個新類。然後逐步重複這一過程，直到並為k類為止。另一種為逐步聚類或稱動態聚類方法。當樣本數很大時，先將n個樣本大致分為k類，然後按照某種最優原則逐步修改，直到分類比較合理為止。
聚類分析是依據個體或變數的數量關係來分類，客觀性較強，但各種聚類方法都只能在某種條件下達到局部最優,聚類的最終結果是否成立,尚需專家的鑑定。必要時可以比較幾種不同的方法，選擇一種比較符合專業要求的分類結果。
主成分分析
把原來多個指標化為少數幾個互不相關的綜合指標的一種統計方法。例如,用p個指標觀測樣本,如何從這p個指標的數據出發分析樣本或總體的主要性質呢？如果p個指標互不相關，則可把問題化為p個單指標來處理。但大多時候p個指標之間存在著相關。此時可運用主成分分析尋求這些指標的互不相關的線性函式，使原有的多個指標的變化能由這些線性函式的變化來解釋。這些線性函式稱為原有指標的主成分，或稱主分量。
主成分分析有助於分辨出影響因變數的主要因素，也可套用於其他多元分析方法，例如在分辨出主成分之後再對這些主成分進行回歸分析、判別分析和典型相關分析。主成分分析還可以作為因素分析的第一步，向前推進就是因素分析。其缺點是只涉及一組變數之間的相互依賴關係，若要討論兩組變數之間的相互關係則須運用典型相關。
典型相關分析
先將較多變數轉化為少數幾個典型變數，再通過其間的典型相關係數來綜合描述兩組多元隨機變數之間關係的統計方法。設x是p元隨機變數,y是q元隨機變數，如何描述它們之間的相關程度?當然可逐一計算x的p個分量和y的q個分量之間的相關係數(p×q個)， 但這樣既繁瑣又不能反映事物的本質。如果運用典型相關分析，其基本程式是，從兩組變數各自的線性函式中各抽取一個組成一對，它們應是相關係數達到最大值的一對，稱為第1對典型變數,類似地還可以求出第2對、第3對、……,這些成對變數之間互不相關,各對典型變數的相關係數稱為典型相關係數。所得到的典型相關係數的數目不超過原兩組變數中任何一組變數的數目。
典型相關分析有助於綜合地描述兩組變數之間的典型的相關關係。其條件是,兩組變數都是連續變數,其資料都必須服從多元常態分配。
以上幾種多元分析方法各有優點和局限性。每一種方法都有它特定的假設、條件和數據要求，例如正態性、線性和同方差等。因此在套用多元分析方法時，應在研究計畫階段確定理論框架，以決定收集何種數據、怎樣收集和如何分析數據資料。
參考書目
張堯庭、方開泰著：《多元統計分析引論》，科學出版社，北京，1982。
丁士晟編著：《多元分析方法及其套用》，吉林人民出版社，長春，1981。
