線性系統代數理論
正文
線性系統理論中用抽象代數的語言和方法研究線性系統的一個理論分支。這種理論和方法的特點是抽象化、形式化和符號化。在這種理論中不採用有直接物理意義的時間域和頻率域的語言，而是把線性系統的模型、運動和各種動態特性採用抽象的代數結構（如群、環、域、模、範疇等）和相應的抽象運算或映射關係來描述。線性系統代數理論的最早的研究是R.E.卡爾曼於1969年創建的模論方法（模是環上的“向量空間”），這個方法後經P.A.富爾曼等人的發展而更趨完善。1972年以後卡爾曼和E.W.卡門等人又把域上的線性系統理論推廣為環上的線性系統理論，獲得一些有意義的結果。後來對這一理論的研究被進一步抽象化，把動態系統（包括線性系統）的研究從不同角度推向更為一般的代數結構領域，使得到的結果具有更大的普遍性。線性系統代數理論最主要的內容是模論方法。基本做法是把參考時刻t＝0以前的輸入序列{u(i)}，i＝-N，－N＋1,…,0（N為正整數）,與一個形式多項式 u(z)＝
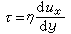相對應,u(z)全體構成輸入模Ω。把t＝1以後的輸出序列 {y(i)}，i＝1，2，…，與一個形式冪級數
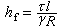相對應,全體y(z)構成輸出模Ψ。每一個u(z)必定與一個y(z)相對應，即從Ω到Ψ有一個映射f，記為f:Ω →Ψ。Ω的商模Ω/ker f（ker f 表示f的核，即映象為零元的u(z)的集合）的每一個元素相當於系統的一個狀態，Ω/kerf 就是系統的狀態空間。在此基礎上，涉及線性系統理論的許多基本問題如能控性、能觀測性、實現問題等都可以用模論的語言表示，並可用代數方法得到一些有意義的結果。模論方法線上性系統理論的研究中很有成效，並已被擴展套用於更為複雜的2-D系統理論等方面的研究中。 環上的線性系統理論是普通的（域上的）線性系統理論的推廣。已有結果表明，環上的線性系統在性能上顯著弱於普通的線性系統。例如，能控性不再是環上的線性系統能任意配置極點的充分條件（見極點配置）。環上的線性系統理論的研究加深了對線性系統的內在規律的認識。
對在其他代數結構上定義的動態系統(包括線性系統)理論也已作了多方面的探討,如群上的自動機、泛代數上的受擾動態系統、半自動機的泛代數描述等。
由於代數方法的抽象性，線性系統的代數理論的結果具有較大的普遍性，適用於很多具體系統，也有助於從代數結構的角度揭示線性系統的數學性質。抽象代數方法還能用於解決某些具體的系統理論問題。例如，可以用完備格理論闡明狀態觀測器的結構。又如，將能控子空間的概念推廣用於計算機形式語言，便產生出能控子語言的概念。此外，代數理論的符號化特點有利於控制理論與計算機科學相結合，為在系統理論研究中使用計算機提供媒介。代數方法的缺點是不能用來解決定量性的細節問題。
參考書目
R.E.Kalman， P.L.Falb and M.A.Arbib， Topics in Mathematical System Theory，McGraw-Hill，NewYork,1969.
凱拉斯著，李清泉等譯：《線性系統》，科學出版社，北京，1985。(T.Kailath,Linear Systems，Prentice-Hall, Inc., Englewood Cliffs., N.J., 1980.)
