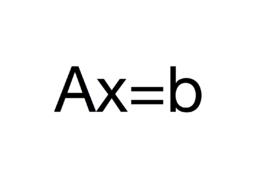非齊次線性方程組

定義

常數項不全為零的線性方程組稱為非齊次線性方程組。

非齊次線性方程組的表達式為：Ax=b

解法

非齊次線性方程組Ax=b的求解步驟：

（1）對增廣矩陣B施行初等行變換化為行階梯形。若R(A)<R(B)，則方程組無解。

（2）若R(A)=R(B)，則進一步將B化為行最簡形。

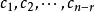非齊次線性方程組

（3）設R(A)=R(B)=r；把行最簡形中r個非零行的非0首元所對應的未知數用其餘n-r個未知數（自由未知數）表示，並令自由未知數分別等於，即可寫出含n-r個參數的通解。

解的存在性

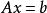非齊次線性方程組

非齊次線性方程組 有解的充分必要條件是：係數矩陣的秩等於增廣矩陣的秩，即rank(A)=rank(A, b)（否則為無解）。

非齊次線性方程組有唯一解的充要條件是rank(A)=n。

非齊次線性方程組有無窮多解的充要條件是rank(A)<n。（rank(A)表示A的秩）

解的結構

非齊次線性方程組的通解=齊次線性方程組的通解+非齊次線性方程組的一個特解（η=ζ+η*）