基本含義
在統計學中,線性回歸(Linear Regression)是利用稱為線性回歸方程的最小平方函式對一個或多個自變數和因變數之間關係進行建模的一種回歸分析。這種函式是一個或多個稱為回歸係數的模型參數的線性組合。只有一個自變數的情況稱為簡單回歸,大於一個自變數情況的叫做多元回歸。(這反過來又應當由多個相關的因變數預測的多元線性回歸區別,而不是一個單一的標量變數。)
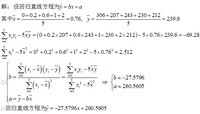 線性回歸
線性回歸 線性回歸
線性回歸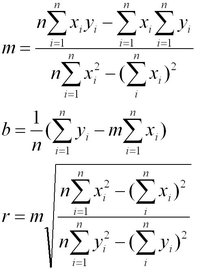 線性回歸
線性回歸 線性回歸
線性回歸回歸分析中,只包括一個自變數和一個因變數,且二者的關係可用一條直線近似表示,這種回歸分析稱為一元線性回歸分析。如果回歸分析中包括兩個或兩個以上的自變數,且因變數和自變數之間是線性關係,則稱為多元線性回歸分析。
線上性回歸中,數據使用線性預測函式來建模,並且未知的模型參數也是通過數據來估計。這些模型被叫做線性模型。最常用的線性回歸建模是給定X值的y的條件均值是X的仿射函式。不太一般的情況,線性回歸模型可以是一個中位數或一些其他的給定X的條件下y的條件分布的分位數作為X的線性函式表示。
 線性回歸
線性回歸線性回歸是回歸分析中第一種經過嚴格研究並在實際套用中廣泛使用的類型。這是因為線性依賴於其未知參數的模型比非線性依賴於其位置參數的模型更容易擬合,而且產生的估計的統計特性也更容易確定。
線性回歸有很多實際用途。分為以下兩大類:
如果目標是預測或者映射,線性回歸可以用來對觀測數據集的和X的值擬合出一個預測模型。當完成這樣一個模型以後,對於一個新增的X值,在沒有給定與它相配對的y的情況下,可以用這個擬合過的模型預測出一個y值。
給定一個變數y和一些變數X1,...,Xp,這些變數有可能與y相關,線性回歸分析可以用來量化y與Xj之間相關性的強度,評估出與y不相關的Xj,並識別出哪些Xj的子集包含了關於y的冗餘信息。
線性回歸模型經常用最小二乘逼近來擬合,但他們也可能用別的方法來擬合,比如用最小化“擬合缺陷”在一些其他規範里(比如最小絕對誤差回歸),或者在橋回歸中最小化最小二乘損失函式的懲罰.相反,最小二乘逼近可以用來擬合那些非線性的模型.因此,儘管“最小二乘法”和“線性模型”是緊密相連的,但他們是不能劃等號的。
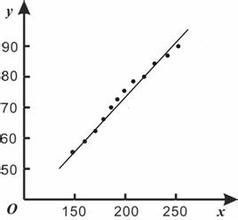
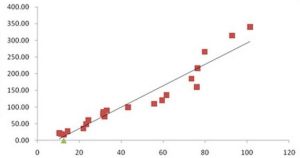
數據組說明線性回歸以一簡單數據組來說明什麼是線性回歸。假設有一組數據型態為 y=y(x),其中x={0, 1, 2, 3, 4, 5}, y={0, 20, 60, 68, 77, 110}。
如果要以一個最簡單的方程式來近似這組數據,則用一階的線性方程式最為適合。先將這組數據繪圖如下。
圖中的斜線是隨意假設一階線性方程式 y=20x,用以代表這些數據的一個方程式。以下將上述繪圖的MATLAB指令列出,並計算這個線性方程式的 y 值與原數據 y 值間誤差平方的總合。
>> x=[0 1 2 3 4 5];
>> y=[0 20 60 68 77 110];
>> y1=20*x; % 一階線性方程式的 y1 值
>> sum_sq = sum((y-y1).^2); % 誤差平方總和為 573
>> axis([-1,6,-20,120])
>> plot(x,y1,x,y,'o'), title('Linear estimate'), grid
如此任意的假設一個線性方程式並無根據,如果換成其它人來設定就可能採用不同的線性方程式;所以必須要有比較精確方式決定理想的線性方程式。可以要求誤差平方的總和為最小,做為決定理想的線性方程式的準則,這樣的方法就稱為最小平方誤差(least squares error)或是線性回歸。MATLAB的polyfit函式提供了 從一階到高階多項式的回歸法,其語法為polyfit(x,y,n),其中x,y為輸入數據組n為多項式的階數,n=1就是一階 的線性回歸法。polyfit函式所建立的多項式可以寫成從polyfit函式得到的輸出值就是上述的各項係數,以一階線性回歸為例n=1,所以只有 二個輸出值。如果指令為coef=polyfit(x,y,n),則coef(1)= , coef(2)=,...,coef(n+1)= 。注意上式對n 階的多 項式會有 n+1 項的係數。看以下的線性回歸的示範:
>> x=[0 1 2 3 4 5];
>> y=[0 20 60 68 77 110];
>> coef=polyfit(x,y,1); % coef 代表線性回歸的二個輸出值
>> a0=coef(1); a1=coef(2);
>> ybest=a0*x+a1; % 由線性回歸產生的一階方程式
>> sum_sq=sum((y-ybest).^2); % 誤差平方總合為 356.82
>> axis([-1,6,-20,120])
>> plot(x,ybest,x,y,'o'), title('Linear regression estimate'), grid。
擬合方程
最小二乘法
一般來說,線性回歸都可以通過最小二乘法求出其方程,可以計算出對於y=bx+a的直線,其經驗擬合方程如下:
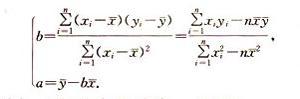 公式
公式其相關係數(即通常說的擬合的好壞)可以用以下公式來計算:
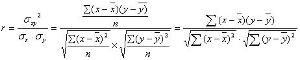 公式
公式結果分析
雖然不同的統計軟體可能會用不同的格式給出回歸的結果,但是它們的基本內容是一致的。以STATA的輸出為例來說明如何理解回歸分析的結果。在這個例子中,測試讀者的性別(gender),年齡(age),知識程度(know)與文檔的次序(noofdoc)對他們所覺得的文檔質量(relevance)的影響。
輸出:
Source | SS df MS Number of obs = 242
-------------+------------------------------------------ F ( 4, 237) = 2.76
Model | 14.0069855 4 3.50174637 Prob > F = 0.0283
Residual | 300.279172 237 1.26700072 R-squared = 0.0446
------------- +------------------------------------------- Adj R-squared = 0.0284
Total | 314.286157 241 1.30409194 Root MSE = 1.1256
------------------------------------------------------------------------------------------------
relevance | Coef. Std. Err. t P>|t| Beta
---------------+--------------------------------------------------------------------------------
gender | -.2111061 .1627241 -1.30 0.196 -.0825009
age | -.1020986 .0486324 -2.10 0.037 -.1341841
know | .0022537 .0535243 0.04 0.966 .0026877
noofdoc | -.3291053 .1382645 -2.38 0.018 -.1513428
_cons | 7.334757 1.072246 6.84 0.000 .
-------------------------------------------------------------------------------------------
輸出
這個輸出包括以下幾部分。左上角給出方差分析表,右上角是模型擬合綜合參數。下方的表給出了具體變數的回歸係數。方差分析表對大部分的行為研究者來講不是很重要,不做討論。在擬合綜合參數中, R-squared 表示因變數中多大的一部分信息可以被自變數解釋。在這裡是4.46%,相當小。
回歸係數
一般地,要求這個值大於5%。對大部分的行為研究者來講,最重要的是回歸係數。年齡增加1個單位,文檔的質量就下降 -.1020986個單位,表明年長的人對文檔質量的評價會更低。這個變數相應的t值是 -2.10,絕對值大於2,p值也<0.05,所以是顯著的。結論是,年長的人對文檔質量的評價會更低,這個影響是顯著的。相反,領域知識越豐富的人,對文檔的質量評估會更高,但是這個影響不是顯著的。這種對回歸係數的理解就是使用回歸分析進行假設檢驗的過程。
回歸誤差
離差平方和
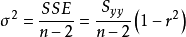 離差平方和 離差平方和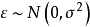 離差平方和 離差平方和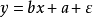 離差平方和 離差平方和 |
其中
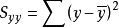 離差平方和
離差平方和代表y的平方和;r^2是相關係數,代表變異被回歸直線解釋的比例;
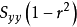 離差平方和
離差平方和根據回歸係數與直線斜率的關係,可以得到等價形式:
 離差平方和
離差平方和利用預測值
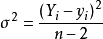 利用預測值
利用預測值不確定度
斜率b
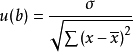 斜率b
斜率b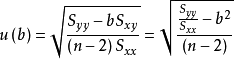 斜率b
斜率b截距a
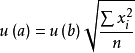 截距a
截距a套用
數學
線性回歸有很多實際用途。分為以下兩大類:
如果目標是預測或者映射,線性回歸可以用來對觀測數據集的和X的值擬合出一個預測模型。當完成這樣一個模型以後,對於一個新增的X值,在沒有給定與它相配對的y的情況下,可以用這個擬合過的模型預測出一個y值。
給定一個變數y和一些變數X1,...,Xp,這些變數有可能與y相關,線性回歸分析可以用來量化y與Xj之間相關性的強度,評估出與y不相關的Xj,並識別出哪些Xj的子集包含了關於y的冗餘信息。
趨勢線
一條趨勢線代表著時間序列數據的長期走勢。它告訴我們一組特定數據(如GDP、石油價格和股票價格)是否在一段時期內增長或下降。雖然我們可以用肉眼觀察數據點在坐標系的位置大體畫出趨勢線,更恰當的方法是利用線性回歸計算出趨勢線的位置和斜率。
流行病學
有關吸菸對死亡率和發病率影響的早期證據來自採用了回歸分析的觀察性研究。為了在分析觀測數據時減少偽相關,除最感興趣的變數之外,通常研究人員還會在他們的回歸模型里包括一些額外變數。例如,假設我們有一個回歸模型,在這個回歸模型中吸菸行為是我們最感興趣的獨立變數,其相關變數是經數年觀察得到的吸菸者壽命。研究人員可能將社會經濟地位當成一個額外的獨立變數,已確保任何經觀察所得的吸菸對壽命的影響不是由於教育或收入差異引起的。然而,我們不可能把所有可能混淆結果的變數都加入到實證分析中。例如,某種不存在的基因可能會增加人死亡的幾率,還會讓人的吸菸量增加。因此,比起採用觀察數據的回歸分析得出的結論,隨機對照試驗常能產生更令人信服的因果關係證據。當可控實驗不可行時,回歸分析的衍生,如工具變數回歸,可嘗試用來估計觀測數據的因果關係。
金融
資本資產定價模型利用線性回歸以及Beta係數的概念分析和計算投資的系統風險。這是從聯繫投資回報和所有風險性資產回報的模型Beta係數直接得出的。
經濟學
線性回歸是經濟學的主要實證工具。例如,它是用來預測消費支出,固定投資支出,存貨投資,一國出口產品的購買,進口支出,要求持有流動性資產,勞動力需求、勞動力供給。