定律定義
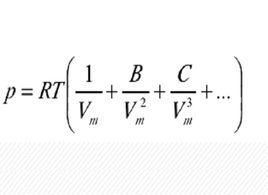
維里方程 的一般表達式：
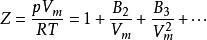維里方程維里方程也可以用壓力p的冪級數來表示
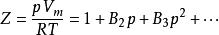維里方程其中V是氣體分子的摩爾體積，計算式：V=V/n；BB分別稱為第二、第三維理係數，它們與氣體的種類有關，而且是溫度的函式，在某一溫度下，維理係數為0，實際氣體行為就和理想氣體近似。而且從以上兩式可以看出摩爾體積越大，氣壓越低，則氣體的行為越趨近於理想氣體。當壓力p→0，體積V→∞時，維里方程還原為理想氣體狀態方程。
推導過程
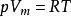維里方程理想氣體狀態方程的表達式： 引入壓縮因子Z，其大小反映出真實氣體對理想氣體的偏差程度，計算定義是Z等於Vm（真實）除以Vm（理想），Z是一個趨近於1的數字，在後面加入級數來進行修正即得到維里方程。
適用範圍
維里方程有堅實的理論基礎。用統計力學方法能導出維里係數，並賦予維里係數明確的物理意義：第二維里係數表示氣體兩個分子相互作用的效應，第三維里係數表示三個分子的相互作用，等。原則上可以從理論上導出各個維里係數的計算式，但實際上高級維里係數的運算是十分困難的，除了簡單的鋼球模型外，還只能算到第三維里係數，通常維里係數由實驗測定。
套用領域
對於液相和汽相，維理狀態方程描述一個 P-V等溫過程更靈活，因為方程有較高次冪的體積、它們比三次狀態方程更精確，普遍化主要是針對烴化合物。因此，對於這些化合物能夠獲得較好的結果，不推薦將它們用於極性化合物
定律影響
維里方程在高密度區的精度不高，但由於具有理論基礎，適應性廣，很有發展前途。B-W-R方程、M-H方程都是在它的基礎上改進得到的。
