特點
(1)只對大量個別偶然事件的總體起作用;
(2)個別偶然事件的數量越多,統計規律性的表現越明顯;
(3)即使對於大量的個別偶然事件的總體來說,也存在所謂漲落現象。
實例
往桌上擲一個硬幣,結果究竟是國徽朝上還是數字朝上,這完全是偶然的,但是如果投擲上千萬次(越多越好),或者一次同時擲成千上萬個(也是越多越好)相同面值的硬幣,那么對所得結果進行統計就會發現,國徽和數字出現的次數大約各占一半。重複做此實驗,結果發現儘管各次國徽朝上的數目有所不同,但基本上是占總數的一半,這就是一種統計規律。
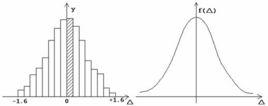
我們還可以用伽耳頓板來演示一種統計規律的現象,如右圖所示,在一塊豎木板的上部規則地頂上很多鐵釘,木板的下部用豎直隔板隔成許多等寬的狹槽板前蓋一塊玻璃。另外,配備一盒小玻璃球(比綠豆還小)作為這套儀器的附屬檔案。實驗時,先每次投入一個小球,我們看到,小球進過與釘子的多次碰撞,最後落進哪一個槽中完全是偶然的。然後每次投入少量小球,則小球在各個槽中的分布情況也是無規律的。但是,當把大量小球倒進伽耳頓板時,則小球在各槽中的分布就出現如右圖中的情況,即在中央槽內的小球最多,而在離中央槽越遠的槽中球越少。反覆做幾次實驗,儘管在某一槽中各次出現的小球數有些出入,但總的說來分布情況仍然如圖所示,這一實驗事實說明,儘管單個小球落到哪一個槽中這一個別現象是偶然的,但大量小球倒進來後在各個槽中的分布這一總體現象卻出現了一種必然性的結果,這也是一種統計規律性。