定義
結合律形式上，一個在集合S上的二元運算 被稱之為 可結合的若其滿足下面的 結合律：
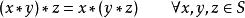結合律。
結合律 結合律運算的順序並不會影響到表示式的值，且可證明這在含有“任意”多個 運算的表示式之下也依然是成立的。因此，當 是可結合的時，運算的順序可以不需要去規範而不會使其意義不清，所以可以省略掉括弧而簡單寫成：
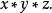結合律不過，需要記住的是，改變運算的順序並不包含或允許以移動表示式中的運算元來改變其真實的運算。
舉例
乘法
乘法結合律：三個數相乘,先把前面兩個數相乘,先乘第三個數,或者先把後面兩個數相乘,再和第一個數相乘,它們的積不變。
字母表示：(a×b)×c=a×(b×c)
集合交並
集合的交，並運算都滿足結合律：
交：（A∩B）∩C=A∩（B∩C）
並：（A∪B）∪C=A∪(B∪C)
矩陣乘法
矩陣乘法滿足結合律。
一個A x B的矩陣乘以一個B x C的矩陣將得到一個A x C的矩陣，時間複雜度為A x B x C。
例子
一些可結合的運算的例子如下。
在算術中，實數的加法和乘法都是可結合的，即：
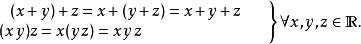結合律複數和四元數的加法與乘法是可結合的。八元數的加法也是可結合的，但其乘法則是不可結合的。
最大公約數和最低公倍數的運算都是可結合的。
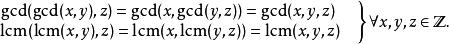結合律因為線性變換是個可表示成矩陣的函式，其中的函式複合則可以用矩陣乘法來表示，立即可知矩陣乘法為可結合的。
集合的交集和並集為可結合的：
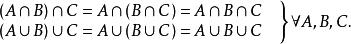結合律若M是某個集合且S為所有從M映射至M的函式所組成的集合，則在S上的函式複合的運算是可結合的：
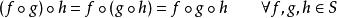結合律。
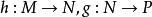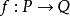結合律
結合律更一般性地，給定四個集合M、N、P和Q，且 、 ，則
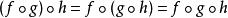結合律和前面一樣。簡單地說，映射的複合總會是可結合的。
給定一個有三個元素A、B和C的集合，其運算如下：
 結合律 | |||
| A | B | C | |
| A | A | A | A |
| B | A | B | C |
| C | A | A | A |
是可結合的。不過，此運算不是可交換的。
不可結合性
一個在集合S上的二元運算*若不滿足結合律，則稱之為 不可結合的。表示成符號即為：
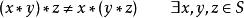結合律。
在此一運算下，運算的順序是 有影響的。減法、除法和冪都是不可結合運算的簡單例子：
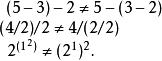結合律一般，當不可結合運算在一個表示出現多於一次時，括弧就必須被使用來表示其運算順序。不過，數學家會對若干常見的不可結合運算採用一種特別的運算順序的規則。這單純只是個為了減少括弧的語法約定。
