有理數加法法則

有理數的加法與國小的加法大有不同，國小的加法不涉及到符號的問題，而有理數的加法運算總是涉及到兩個問題：一是確定結果的符號；二是求結果的絕對值。 在進行有理數加法運算時，首先判斷兩個加數的符號：是同號還是異號，是否有0。從而確定用那一條法則。在套用過程中，一定要牢記"先符號，後絕對值",熟練以後就不會出錯了。 多個有理數的加法，可以從左向右計算，也可以用加法的運算定律計算，但是在下筆前一定要思考好，哪一個要用定律哪一個要從左往右計算。

基本信息

• 中文名：有理數加法法則
• 英文名：Law of rational number addition

• 組成：交換律和結合律
• 學科：數學

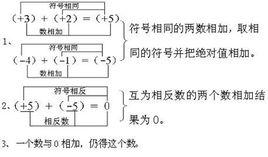
法則

同號兩數相加，取相同的符號,並把絕對值相加。異號兩數相加，絕對值相等時，和為零；絕對值不等時，取絕對值較大的數的符號，並用較大的絕對值減去較小的絕對值；一個數同零相加仍得這個數。

交換律和結合律

1、有理數的加法同樣擁有交換律和結合律(和整數得交換律和結合律一樣)用字母表示為:

交換律:a+b=b+a 兩個數相加，交換加數的位置，和不變。

結合律:a+b+c=(a+b)+c=a+(b+c)。

2、三個數相加，先把前兩個數相加，或者先把後兩個數相加，和不變。

要點

同號相加不變,異號相加變減.欲問符號怎么定,絕對值大號選。

在進行有理數加法運算時，一般採取：1.是互為相反數的先加（抵消）；2.同號的先加；3.同分母的先加；4.能湊整數的先加;5.異分母分數相加,先通分,再計算.6.幾個數相加能得到整數的可以先相加。