定義
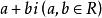純虛數
純虛數形如的數叫作 複數，其中是複數的實部，b是複數的虛部，全體複數組成的集合叫作複數集，用字母 C表示。
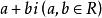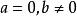純虛數
純虛數複數，當b=0時，就是實數；當b≠0時，叫作 虛數；當時．叫作 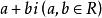純虛數。
純虛數把複數表示成的形式，叫作複數的代數形式。
幾何意義
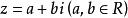純虛數從複數相等的定義我們知道，任何一個複數都可以用一個有序實數對(a，b)唯一確定，這樣我們可以用建立了直角坐標系的平面來表示複數。
建立了直角坐標系來表示複數的平面叫作 複平面，x軸叫作實軸，y軸叫作虛軸，這樣，實軸上的點都表示實數，除了原點外， 虛軸上的點都表示純虛數。
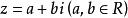純虛數
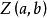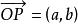純虛數
純虛數複數與複平面內的點及向量是一一對應的，複數的模表示複數對應的點到原點的距離。
判別
實數、虛數、純虛數的判別方法
學習了純虛數的定義以後，通過這類題來鞏固對純虛數的理解，請看例題．
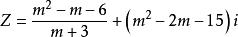純虛數例題:m為何實數時，複數是實數?虛數?純虛數?
分析：要明確什麼是複數的實部與虛部?何時它們有意義?何時它們為零或非零?從而由實數、虛數、純虛數分別對實部與虛部的要求進行討論。
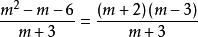純虛數
純虛數解：實部：。
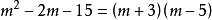純虛數虛部：。
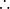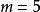純虛數
純虛數當時，Z是實數；
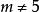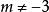純虛數
純虛數當 且時，Z是虛數；
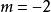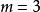純虛數
純虛數當或時，Z是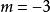純虛數。
純虛數說明：當時，實部無意義，在討論過程中應排除掉。
小結：對這類題可歸納為如下題型。
欲判別複數
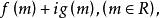純虛數可化為解代數方程或不等式。
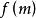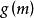純虛數
純虛數在實部、虛部都有定義的前提下：
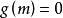純虛數實數(對應點在實軸上)；；
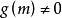純虛數虛數(對應點不在實軸上)：；
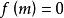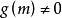純虛數 純虛數純虛數(對應點在虛軸上)：且;
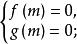純虛數對應點在原點：解方程組
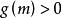純虛數對應點在實軸上方：解不等式
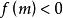純虛數對應點在虛軸左側：解不等式；
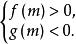純虛數對應點在複平面的第一象限內：解不等式組
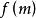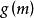純虛數 純虛數其他情況類推．但應注意所討論的範圍必須在、的定義域內。
