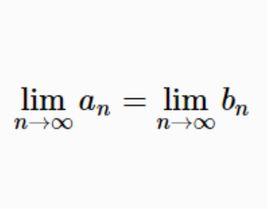基本介紹
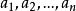算術幾何平均算術幾何平均不等式n個正數的算術平均
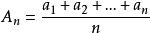算術幾何平均不小於它們的幾何平均
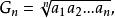算術幾何平均即
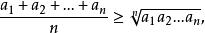算術幾何平均
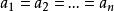算術幾何平均式中若且唯若時取等號 。
算術幾何平均
算術幾何平均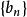算術幾何平均設a和b是兩個正數，定義數列和如下
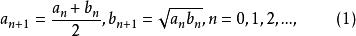算術幾何平均
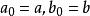算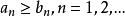術幾何平均
算術幾何平均 算術幾何平均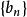 算術幾何平均這裡。由算術幾何平均不等式，明顯地，．根據數學歸納法容易證明數列是遞減的，而是遞增的，等價於
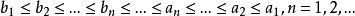算術幾何平均清楚地，
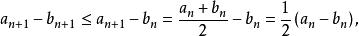算術幾何平均進而得到
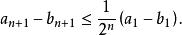算術幾何平均因此，這兩個數列有共同的極限，即
算術幾何平均
算術幾何平均我們稱該極限為a和b的 算術-幾何平均AGM(a，b)，也有一些文獻用AG(a，b)表示這個平均.。Lagrange和Gauss首先研究了這個平均，但是這個平均真正的重要性以及與橢圓積分的聯繫屬於Gauss，有時也稱這個平均為Gauss算術-幾何平均 。
相關結論
設
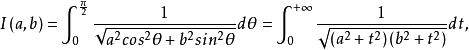算術幾何平均定理 (Gauss)
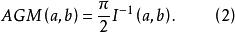算術幾何平均
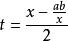算術幾何平均證明 作變數代換，則
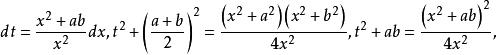算術幾何平均因此，
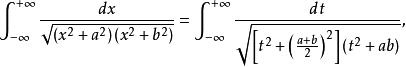算術幾何平均
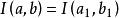算術幾何平均
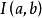算術幾何平均
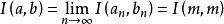算術幾何平均也就是說，我們獲得。根據歸納法，並注意到是(a，b)的連續函式，我們得到，這裡m=AGM(a，b)，清楚地，
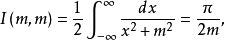算術幾何平均因此(2)式成立。(2)中的兩個積分稱為橢圓積分。給出AGM的運算規則(1)稱為Gauss運算規則 。
