幾何平均法

就是運用幾何平均數求出預測目標的發展速度，然後進行預測。它適用預測目標發展過程一貫上升或下降，且逐期環比率速度大體接近的情況。是n個價格變數連乘積的n次方根。 在統計研究中常用以計算平均發展速度。在計算不同時期年度平均價格上漲幅度時，也用這種方法。

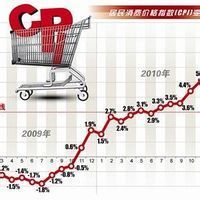
基本概述

現象發展的平均速度，一般用幾何平均法計算。按幾何平均法求平均發展速度，需要藉助於對數來計算。但在實際工作中，我們統計工作者常用兩種工具來計算，一種是用多功能電子計算器計算；另一種是查《水平法查對表》。這種查對數在已知“總速度”和“間隔期”的情況下，可以直接查到平均增長速度。

幾何平均數（Geometric mean）

幾何平均數的概念

幾何平均數是n個變數值連乘積的n次方根。

幾何平均數多用於計算平均比率和平均速度。如：平均利率、平均發展速度、平均合格率等。

相關特點

1、幾何平均數受極端值的影響較算術平均數小。

2、如果變數值有負值，計算出的幾何平均數就會成為負數或虛數。

3、它僅適用於具有等比或近似等比關係的數據。

4、幾何平均數的對數是各變數值對數的算術平均數。

套用舉例

假定某地儲蓄年利率（按複利計算）：5%持續1.5年，3%持續2.5年，2.2%持續1年。請問此5年內該地平均儲蓄年利率。該地平均儲蓄年利率