等角共軛

三角形內部點的等角共軛變換

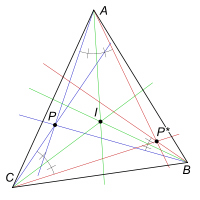
點 P 的等角共軛

幾何學中，設點P是三角形ABC平面上一點，作直線PA、PB和PC分別關於角A 、B和C的平分線的反射，這三條反射線必然交於一點[1]，稱此點為P關於三角形ABC的等角共軛。 （這個定義只對點，不是對三角形ABC的邊。）
點P的等角共軛點經常記作P*，顯然P*的等角共軛點即為P。
內心I的等角共軛點是自身。垂心H的等角共軛點是外心O。重心的等角共軛點是類似重心K。
在三線坐標中，如果X = x : y : z是不在三角形ABC邊上的一點，那么它的等角共軛是1/x : 1/y : 1/z。因此，X的等角共軛有時也記作X −1。三角形內部的點集S在三線乘法
(p : q : r) * (u : v : w) = pu : qv : rw，
下構成一個交換群。 S中任何一點X的逆是X −1。
因為等角共軛是一個函式，從而我們可以討論一個點集的等角共軛。譬如，直線的等角共軛是一條外接圓錐曲線；確切的，若直線交外接圓於0、1或2點，其等角共軛分別為橢圓、拋物線或雙曲線。外接圓的等角共軛是無窮遠直線。一些有名的三次曲線（例如：Thompson三次曲線、Darboux三次曲線、Neuberg三次曲線）是自等角共軛的，即如果X位於這些三次曲線上，那么X −1也在其上。