等角共軛點

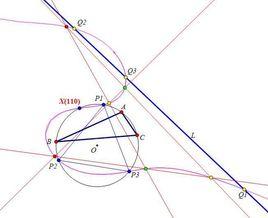
描述

描述一：三角形內一點P，過A做直線L與AP關於角A的角平分線對稱，同樣過B,C分別做L,L。這三條直線交於P，則P是P的等角共軛點；

描述二：設P、Q是三角形ABC內兩點，∠PAB=∠QAC,∠PBC=∠QBA,∠PCB=∠QCA，滿足題設條件的兩點P、Q稱為△ABC的等角共軛點。

記號

幾何學中，設點 P是三角形 ABC平面上一點，作直線 PA、 PB和 PC分別關於角 A、 B和 C的平分線的反射，這三條反射線必然交於一點，稱此點為 P關於三角形 ABC的 等角共軛。（這個定義只對點，不是對三角形 ABC的邊。）

點 P的等角共軛點經常記作 P*，顯然 P*的等角共軛點即為 P。

性質

1.重心的等角共軛點到三角形的三邊的距離的平方和最小。

2.外接圓上一點的等角共軛點是無窮遠點。反過來也成立（摘自詹森《近代歐氏幾何學》）

3.從兩個等角共軛點到各邊的垂線的垂足在一個圓上，即等角共軛點有一個公共的垂足圓，圓心是二者連線中點。（摘自詹森《近代歐氏幾何學》）

4.一點的垂足三角形的邊，垂直於原三角形相應頂點與這點的等角共軛市點的連線。（摘自詹森《近代歐式幾何學》）

5.設P，Q為等角共軛點。則：

∠APA+∠AQA=∠AAA.（摘自詹森《近代歐氏幾何學》）

6.設任一圓交三角形邊於P、Q、P、Q、P、Q，則三個點的組PPP與QQQ的密克點P與Q即為等角共軛點。（摘自詹森《近代歐式幾何學》）

套用

內心 I的等角共軛點是自身。垂心 H的等角共軛點是外心 O。重心的等角共軛點是類似重心 K。

在三線坐標中，如果 X= x: y: z是不在三角形 ABC邊上的一點，那么它的等角共軛是 1/ x: 1/ y: 1/ z。因此， X的等角共軛有時也記作 X。三角形內部的點集 S在三線乘法

(p:q:r) * (u:v:w) = pu:qv:rw，

下構成一個交換群。 S中任何一點 X的逆是 X。

因為等角共軛是一個函式，從而我們可以討論一個點集的等角共軛。譬如，直線的等角共軛是一條外接圓錐曲線；確切的，若直線交外接圓於 0、1或 2 點，其等角共軛分別為橢圓、拋物線或雙曲線。外接圓的等角共軛是無窮遠直線。一些有名的三次曲線（例如：Thompson 三次曲線、Darboux 三次曲線、Neuberg 三次曲線）是自等角共軛的，即如果 X 位於這些三次曲線上，那么 X也在其上。