概念
自然數冪求和公式是清朝數學家李善蘭先生在他的著作《垛積比類》中提出的一種數列求和公式。
公式
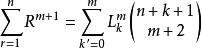自然數冪求和公式公式具體內容:
自然數冪求和公式推導
它不是一個等差數列，也不是一個等比數列，但通過二項式定理的展開式，可以轉化為按等差數列，由低次冪到高次冪遞進求和，最終可推導至李善蘭自然數冪求和公式的原形。
當n為奇數時，由1 +2 +3 +...+N 與s=N +(N-1) +(N-2) +...+1 相加得:
2s=N +[1 +(N-1) ]+[2 +(N-2) ]+[3 +(N-3) ]+...+[(N-1) +(N-N-1) ]+N
=N +N +N +...+N 加或減去所有添加的二項式展開式數
=(1+N)N 減去所有添加的二項式展開式數。
當n為偶數時，由1 +2 +3 +...+N 與s=N +(N-1) +(N-2) +...+1 相加得:
2s=N +[1 +(N-1) ]+[2 +(N-2) ]+[3 +(N-3) ]+...+[(N-1) +(N-N-1) ]+N
=2N +2[(N-2) +(N-4) +(N-6) +...0或1]加或減去所有添加的二項式展開式數
又當n為偶數時，由1 +2 +3 +...+N 與s=N +(N-1) +(N-2) +...+1 相加得:
2s=[N +1 ]+[(N-1) +2 ]+[(N-2) +3 ]+...+[(N-N-1) +(N-1) ]
=2[(N-1) +(N-3) +(N-5) +...0或1]加或減去所有添加的二項式展開式數,合併n為偶數時2S的兩個計算結果，可以得到s=N +(N-1) +(N-2) +...+1的計算公式。
其中，所有添加的二項式展開式數，按下列二項式展開式確定，如此可以順利進行自然數的1至n冪的求和公式的遞進推導。 （最終推導至李善蘭自然數冪求和公式）
