術語簡介
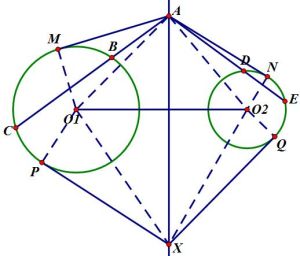 等差冪線
等差冪線PM⊥AB的充要條件是:
若PM⊥AB,則有AP^2一AM^2=BP^2一BM^2。
實現過程
證明:AP^2一AN^2=PN^2;
AM^2一AN^2=MN^2
以上兩式相減得
①
同理,
BP^2一BM^2=PN^2一MN^2②
由式①、②得
AP^2一AM^2=BP^2一BM^2③
證畢。
反之,若有AP^2一AM^2=BP^2一BM^2成立,則PM⊥AB。
證明:設∠ANP=α,則∠BNP=π—α
故AP^2一AM^2
=AN^2+PN^2—2AN·PNcosα+2AN·MNcosα一AN^2一MN^2
=PN^2一MN^2一2AN·PNcosα+2AN·MNcosα
BP^2一BM^2
=PN^2+BN^2一2PN·BNcos(π—α)一MN^2一BN^2+2MN·BNcos(π—α).
=PN^2一MN^2+2PN·BNcosα一2MN·BNcosα
由式③得
2AN·MNcosα一2AN·PNcosα
=2PN·BNcosα一2MN·BNcosα,
即MN(AN+BN)cosα
=PN(AN+BN)cosα
從而,(PN一MN)cosα=0,即PMcosα=0
因此,cosα=0
又因為0<α<π,所以α=π/2
故PM⊥AB

