公理
公理1
如果一條直線上的兩點在一個平面內,那么這條直線上的所有點都在這個平面內。
(1)判定直線在平面內的依據
(2)判定點在平面內的方法
公理2
如果兩個不重合的平面有一個公共點,那么它們有且僅有一條經過該點的公共直線 。
(1)判定兩個平面相交的依據
(2)判定若干個點在兩個相交平面的交線上
公理3
經過不在一條直線上的三點,有且只有一個平面。
(1)確定一個平面的依據
(2)判定若干個點共面的依據
推論
推論1
經過一條直線和這條直線外一點,有且僅有一個平面。
(1)判定若干條直線共面的依據
(2)判斷若干個平面重合的依據
(3)判斷幾何圖形是平面圖形的依據
推論2
經過兩條相交直線,有且僅有一個平面。
推論3
經過兩條平行線,有且僅有一個平面。
其他理論
空間二直線平行直線
平行公理:平行於同一直線的兩條直線互相平行
等角定理:如果一個角的兩邊和另一個角的兩邊分別平行,並且方向相同,那么這兩個角相等。
異面直線
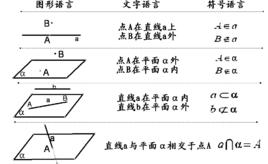
空間直線和平面位置關係
(1)直線在平面內——有無數個公共點
(2)直線和平面相交——有且只有一個公共點
(3)直線和平面平行——沒有公共點
直線與平面所成的角
(1)平面的斜線和它在平面上的射影所成的銳角,叫做這條斜線與平面所成的角
(2)一條直線垂直於平面,定義這直線與平面所成的角是直角
(3)一條直線和平面平行,或在平面內,定義它和平面所成的角是00的角
三垂線定理 在平面內的一條直線,如果和這個平面的一條斜線的射影垂直,那么它和這條斜線垂直
三垂線逆定理 在平面內的一條直線,如果和這個平面的一條斜線垂直,那么它和這條斜線的射影垂直
空間兩個平面 兩個平面平行 判定
性質
(1)如果一個平面內有兩條相交直線平行於另一個平面,那么這兩個平面平行
(2)垂直於同一直線的兩個平面平行
(1)兩個平面平行,其中一個平面內的直線必平行於另一個平面
(2)如果兩個平行平面同時和第三個平面相交,那么它們的交線平行
(3)一條直線垂直於兩個平行平面中的一個平面,它也垂直於另一個平面
相交的兩平面 二面角:從一條直線出發的兩個半平面所組成的圖形叫做二面角,這條直線叫二面角的線,這兩個半平面叫二面角的面
二面角的平面角:以二面角的棱上任一點為端點,在兩個面內分另作垂直棱的兩條射線,這兩條射線所成的角叫二面角的平面角
平面角是直角的二面角叫做直二面角
兩平面垂直 判定
性質
如果一個平面經過另一個平面的一條垂線,那么這兩個平面互相垂直
(1)若二平面垂直,那么在一個平面內垂直於它們的交線的直線垂直於另一個平面
(2)如果兩個平面垂直,那么經過第一個平面內一點垂直於第二個平面的直線,在第一個平面內
立體幾何 多面體、稜柱、稜錐
多面體
定義 由若干個多邊形所圍成的幾何體叫做多面體。
稜柱 斜稜柱:側棱不垂直於底面的稜柱。
直稜柱:側棱與底面垂直的稜柱。
正稜柱:底面是正多邊形的直稜柱。
稜錐 正稜錐:如果稜錐的底面是正多邊形,並且頂點在底面的射影是底面的中心,這樣的稜錐叫正稜錐。
球
到一定點距離等於定長或小於定長的點的集合。
歐拉定理
簡單多面體的頂點數V,棱數E及面數F間有關係:V+F-E=2