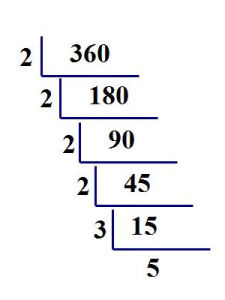
基本定義
求最大公約數的一種方法,也可用來求最低公倍數。求幾個數最大公約數的方法,開始時用觀察比較的方法,即:先把每個數的約數找出來,然後再找出公約數,最後在公
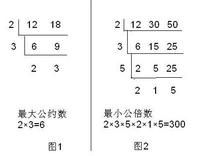 短除法
短除法約數中找出最大公約數。
基本方法
短除符號就是除號倒過來。短除就是在除法中寫除數的地方寫兩個數共有的質因數,然後落下兩個數被公有質因數整除的商,之後再除,以此類推,直到結果互質為止(兩兩互質)。
注意問題
在用短除計算多個數時,對其中任意兩個數存在的因數都要算出,其它沒有這個因數的數則原樣落下。直到剩下每兩個都是互質關係。求最大公約數便乘一邊,求最小公被數便乘一半。這種方法對求兩個以上數的最大公因數,特別是數目較大的數,顯然是不方便的。於是又採用了給每個數分別分解質因數的方法。
舉例說明
例如:求12與18的最大公約數。 短除法例題
短除法例題12的約數有:1、2、3、4、6、12。
18的約數有:1、2、3、6、9、18。
12與18的公約數有:1、2、3、6。
12與18的最大公約數是6。
這種方法對求兩個以上數的最大公約數,特別是數目較大的數,顯然是不方便的。於是又採用了給每個數分別分解質因數的方法。
12=2×2×3
18=2×3×3
12與18都可以分成幾種形式不同的乘積,但分成質因數連乘積就只有以上一種,而且不能再分解了。所分出的質因數無疑都能整除原數,因此這些質因數也都是原數的約數。從分解的結果看,12與18都有公約數2和3,而它們的乘積2×3=6,就是 12與18的最大公約數。
採用分解質因數的方法,也是採用短除的形式,只不過是分別短除,然後再找公約數和最大公約數。如果把這兩個數合在一起短除,則更容易找出公約數和最大公約數。
從短除中不難看出,12與18都有公約數2和3,它們的乘積2×3=6就是12與18的最大公約數。與前邊分別分解質因數相比較,可以發現:不僅結果相同,而且短除法豎式左邊就是這兩個數的公共質因數,而兩個數的最大公約數,就是這兩個數的公共質因數的連乘積。
實際套用中,是把需要計算的兩個或多個數放置在一起,進行短除。
在計算多個數的最低公倍數時,對其中任意兩個數存在的約數都要算出,其它無此約數的數則原樣落下。最後把所有約數和最終剩下無法約分的數連乘即得到最低公倍數。