基本性質
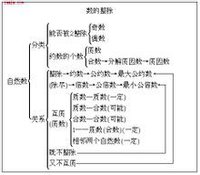 整除抽象圖
整除抽象圖①若a|b,a|c,則a|(b±c)。
②若a|b,則對任意c,a|bc。
③對任意非零整數a,±1|a,±a|a。
④若a|b,b|a,則|a|=|b|。
⑤如果a能被b整除,c是任意整數,那么積ac也能被b整除。
⑥如果a同時被b與c整除,並且b與c互質,那么a一定能被積bc整除,反過來也成立。
對任意整數a,b,b>0,存在唯一的數對q,r,使a=bq+r,其中0≤r
若c|a,c|b,則稱c是a,b的公因數。若d是a,b的公因數,d≥0,且d可被a,b的任意公因數整除,則d是a,b的最大公因數。若a,b的最大公因數等於1,則稱a,b互素,也稱互質。累次利用帶餘除法可以求出a,b的最大公因數,這種方法常稱為輾轉相除法。又稱歐幾里得算法。
數的特徵
常用辨別方法
(1)1與0的特性:
1是任何整數的約數,即對於任何整數a,總有1|a.
0是任何非零整數的倍數,a≠0,a為整數,則a|0.
(2)能被2整除的數的特徵
若一個整數的末位是0、2、4、6或8,則這個數能被2整除。
(3)能被3整除的數的特徵
1,若一個整數的數字和能被3整除,則這個整數能被3整除。
2,由相同的數字組成的三位數、六位數、九位數……這些數字能被3整除。如111令3整除。
(4)能被4整除的數的特徵
若一個整數的末尾兩位數能被4整除,則這個數能被4整除。
(5)能被5整除的數的特徵
若一個整數的末位是0或5,則這個數能被5整除。
(6)能被6整除的數的特徵
若一個整數能被2和3整除,則這個數能被6整除。
(7)能被7整除的數的特徵
若一個整數的個位數字截去,再從餘下的數中,減去個位數的2倍,如果差是7的倍數,則原數能被7整除。如果差太大或心算不易看出是否7的倍數,就需要繼續上述「截尾、倍大、相減、驗差」的過程,直到能清楚判斷為止。同能被17整除的數的特徵。
(8)能被8整除的數的特徵
若一個整數的末尾三位數能被8整除,則這個數能被8整除。
(9)能被9整除的數的特徵
若一個整數的數字和能被9整除,則這個整數能被9整除。
(10)能被10整除的數的特徵
若一個整數的末位是0,則這個數能被10整除。
(11)能被11整除的數的特徵
若一個整數的奇位數字之和與偶位數字之和的差能被11整除,則這個數能被11整除。11的倍數檢驗法也可用上述檢查7的「割尾法」處理!過程唯一不同的是:倍數不是2而是1!
(12)能被12整除的數的特徵
若一個整數能被3和4整除,則這個數能被12整除。
其他辨別方法
(13)能被13整除的數的特徵
若一個整數的個位數字截去,再從餘下的數中,加上個位數的4倍,如果和是13的倍數,則原數能被13整除。如果和太大或心算不易看出是否13的倍數,就需要繼續上述「截尾、倍大、相加、驗和」的過程,直到能清楚判斷為止。
(14)能被17整除的數的特徵
1、若一個整數的個位數字截去,再從餘下的數中,減去個位數的5倍,如果差是17的倍數,則原數能被17整除。如果差太大或心算不易看出是否17的倍數,同能被7整除的特徵一樣。
2、若一個整數的末三位與3倍的前面的隔出數的差能被17整除,則這個數能被17整除。
(15)能被19整除的數的特徵
1、若一個整數的個位數字截去,再從餘下的數中,加上個位數的2倍,如果和是19的倍數,則原數能被19整除。如果和太大或心算不易看出是否19的倍數,就需要繼續使用能被13整除特徵的方法。
2、若一個整數的末三位與7倍的前面的隔出數的差能被19整除,則這個數能被19整除。
(16)能被23整除的數的特徵
若一個整數的末四位與前面5倍的隔出數的差能被23(或29)整除,則這個數能被23整除。
統一方法
設整數x的個位數為a,判斷其是否能被n整除:令(x-a)/10-ma=nk(k∈N*),則x=n[10k+(10m+1)a/n],要使x能被n整除,只要(10m+1)/n為自然數。
舉例
整除規則第七條(7):把個位數字截去,再從餘下的數中,減去個位數的2倍,差是7的倍數,則原數能被7整除。
例:
①147,截去個位數字後為14,用14-7*2=0,0是7的倍數,所以147也是7的倍數。
②2198,截去個位數字後為219,用219-8*2=203;繼續下去,截去個位數字後為20,用20-3*2=14,14是7的倍數,所以2198也是7的倍數。
證明
設p=a1+a2*10+a3*10^2+...+a(n-1)*10^(n-1)+an*10^n
q=a2+a3*10+...+a(n-1)*10^(n-2)+an*10^(n-1)-2a1
2p+q=21(a2+a3*10+...+an*10^(n-1))
又因為21=7*3,所以若p是7的倍數,那么可以得到q是7的倍數。

