基本概念
如果數a能被數b整除,a就叫做b的倍數,b就叫做a的約數。約數和倍數都表示一個整數與另一個整數的關係,不能單獨存在。如只能說16是某數的倍數,2是某數的約數,而不能孤立地說16是倍數,2是約數。
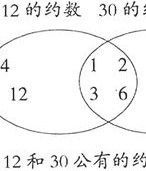 最大公約數
最大公約數"倍"與"倍數"是不同的兩個概念,"倍"是指兩個數相除的商,它可以是整數、小數或者分數。"倍數"只是在數的整除的範圍內,相對於"約數"而言的一個數字的概念,表示的是能被某一個自然數整除的數。
幾個整數,公有的約數,叫做這幾個數的公約數;其中最大的一個,叫做這幾個數的最大公約數。例如:12、16的公約數有±1、±2、±4,其中最大的一個是4,4是12與16的最大公約數,一般記為(12、16)=4。12、15、18的最大公約數是3,記為(12、15、18)=3。
幾個自然數公有的倍數,叫做這幾個數的公倍數,其中最小的一個自然數,叫做這幾個數的最低公倍數。例如:4的倍數有±4、±8、±12、±16,……,6的倍數有±6、±12、±18、±24,……,4和6的公倍數有±12、±24,……,其中最小的是12,一般記為[4,6]=12。12、15、18的最低公倍數是180。記為[12,15,18]=180。若干個互質數的最低公倍數為它們的乘積的絕對值。
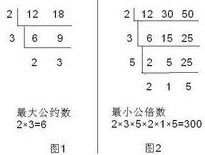 最大公約數
最大公約數求法
質因數分解法
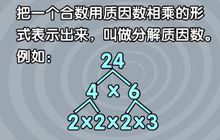 質因數分解
質因數分解質因數分解法:把每個數分別分解質因數,再把各數中的全部公有質因數提取出來連乘,所得的積就是這幾個數的最大公約數。
例如:求24和60的最大公約數,先分解質因數,得24=2×2×2×3,60=2×2×3×5,24與60的全部公有的質因數是2、2、3,它們的積是2×2×3=12,所以,(24、60)=12。
把幾個數先分別分解質因數,再把各數中的全部公有的質因數和獨有的質因數提取出來連乘,所得的積就是這幾個數的最低公倍數。
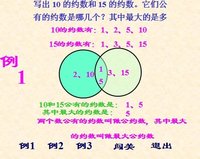
例如:求6和15的最低公倍數。先分解質因數,得6=2×3,15=3×5,6和15的全部公有的質因數是3,6獨有質因數是2,15獨有的質因數是5,2×3×5=30,30裡面包含6的全部質因數2和3,還包含了15的全部質因數3和5,且30是6和15的公倍數中最小的一個,所以[6,15]=30。
短除法
短除法:短除法求最大公約數,先用這幾個數的公約數連續去除,一直除到所有的商互質為止,然
後把所有的除數連乘起來,所得的積就是這幾個數的最大公約數。
短除法求最低公倍數,先用這幾個數的公約數去除每個數,再用部分數的公約數去除,並把不能整除的數移下來,一直除到所有的商中每兩個數都是互質的為止,然後把所有的除數和商連乘起來,所得的積就是這幾個數的最低公倍數,例如,求12、15、18的最低公倍數。
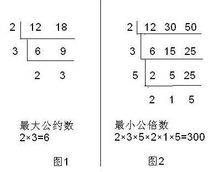 短除法的格式
短除法的格式短除法的本質就是質因數分解法,只是將質因數分解用短除符號來進行。
短除符號就是除號倒過來。短除就是在除法中寫除數的地方寫兩個數共有的質因數,然後落下兩個數被公有質因數整除的商,之後再除,以此類推,直到結果互質為止(兩個數互質)。
而在用短除計算多個數時,對其中任意兩個數存在的因數都要算出,其它沒有這個因數的數則原樣落下。直到剩下每兩個都是互質關係。
求最大公因數便乘一邊,求最低公倍數便乘一圈。
無論是短除法,還是分解質因數法,在質因數較大時,都會覺得困難。這時就需要用新的方法。
輾轉相除法
 古希臘數學家歐幾里德
古希臘數學家歐幾里德輾轉相除法:輾轉相除法是求兩個自然數的最大公約數的一種方法,也叫歐幾里德算法。
這就是輾轉相除法的原理。
 輾轉相除法的格式
輾轉相除法的格式例如,求(319,377):
∵ 319÷377=0(餘319)
∴(319,377)=(377,319);
∵ 377÷319=1(餘58)
∴(377,319)=(319,58);
∵ 319÷58=5(餘29),
∴ (319,58)=(58,29);
∵ 58÷29=2(餘0),
∴ (58,29)= 29;
∴ (319,377)=29.
可以寫成右邊的格式。
用輾轉相除法求幾個數的最大公約數,可以先求出其中任意兩個數的最大公約數,再求這個最大公約數與第三個數的最大公約數,依次求下去,直到最後一個數為止。最後所得的那個最大公約數,就是所有這些數的最大公約數。
更相減損法
 劉徽《九章算術》
劉徽《九章算術》更相減損法:也叫更相減損術,是出自《九章算術》的一種求最大公約數的算法,它原本是為約分而設計的,但它適用於任何需要求最大公約數的場合。
《九章算術》是中國古代的數學專著,其中的“更相減損術”可以用來求兩個數的最大公約數,即“可半者半之,不可半者,副置分母、子之數,以少減多,更相減損,求其等也。以等數約之。”
翻譯成現代語言如下:
第一步:任意給定兩個正整數;判斷它們是否都是偶數。若是,則用2約簡;若不是則執行第二步。
第二步:以較大的數減較小的數,接著把所得的差與較小的數比較,並以大數減小數。繼續這個操作,直到所得的減數和差相等為止。
則第一步中約掉的若干個2與第二步中等數的乘積就是所求的最大公約數。
其中所說的“等數”,就是最大公約數。求“等數”的辦法是“更相減損”法。所以更相減損法也叫等值算法。
例1、用更相減損術求98與63的最大公約數。
解:由於63不是偶數,把98和63以大數減小數,並輾轉相減:
98-63=35
63-35=28
35-28=7
28-7=21
21-7=14
14-7=7
所以,98和63的最大公約數等於7。
這個過程可以簡單的寫為:
(98,63)=(35,63)=(35,28)=(7,28)=(7,21)=(7,14)=(7,7)=7.
例2、用更相減損術求260和104的最大公約數。
解:由於260和104均為偶數,首先用2約簡得到130和52,再用2約簡得到65和26。
此時65是奇數而26不是奇數,故把65和26輾轉相減:
65-26=39
39-26=13
26-13=13
所以,260與104的最大公約數等於13乘以第一步中約掉的兩個2,即13*2*2=52。
這個過程可以簡單地寫為:
(260,104)=(65,26)=(39,26)=(13,26)=(13,13)=13.
比較輾轉相除法與更相減損術的區別
(1)都是求最大公因數的方法,計算上輾轉相除法以除法為主,更相減損術以減法為主,計算次數上輾轉相除法計算次數相對較少,特別當兩個數字大小區別較大時計算次數的區別較明顯。
(2)從結果體現形式來看,輾轉相除法體現結果是以相除餘數為0則得到,而更相減損術則以減數與差相等而得到。
歷史發展
 古希臘數學家歐多克斯
古希臘數學家歐多克斯在求解最大公約數的幾種方法中,輾轉相除法最為出名。輾轉相除法是目前仍然在使用的歷史最悠久的算法之一。它首次出現於幾何原本(卷7命題1–2、卷10命題2–3)(大約公元前300年)。在卷7中用於整數,在卷10中用於線段的長度(也就是現在所說的實數,但是當時未有實數的概念)。卷10中出現的算法是幾何的,兩段線段a和b的最大公約數是準確測量a和b的最大長度。
這個算法可能並非歐幾里得發明,而僅僅是將先人的結果編進他的幾何原本。數學家、歷史學家范德瓦爾登認為卷7的內容可能來自畢達哥拉斯學院出身的數學家寫的關於數論的教科書。輾轉相除法可能是被大約公元前375年的歐多克斯發現的,但也有可能更早之前就已經存在,因為歐幾里得和亞里士多德的著作中都出現了ἀνθυφαίρεσις一詞(anthyphairesis, 意為“輾轉相減”),
 中國的秦九韶
中國的秦九韶幾個世紀之後,輾轉相除法又分別被中國人和印度人獨立發現,主要用來解天文學中用到的丟番圖方程以及指定準確的曆法。5世紀末,印度數學家、天文學家阿里亞哈塔可能是因為輾轉相除法在解丟番圖方程時的高效率而稱它為“粉碎機”。因為在中國,孫子算經中出現了此算法的一個特例中國剩餘定理,但是輾轉相除法的完整表述直到1247年秦九韶的數學九章中才出現。在歐洲,輾轉相除法首次出現於克勞德·巴希特(英語:Claude Gaspard Bachet de Méziriac)的著作Problèmes plaisants et délectables的第二版在歐洲,輾轉相除法廣泛使用於丟番圖方程和連分數。後來,英國數學家桑德森(英語:Nicholas Saunderson)將擴展歐幾里得算法作為羅傑科茨(英語:Roger Cotes)對計算連分數的方法的研究發表。
 德國數學家狄利克雷
德國數學家狄利克雷19世紀,輾轉相除法孕育出了一些新的數系,如高斯整數和艾森斯坦整數。1815年,高斯用輾轉相除法證明高斯整數的分解是惟一的,他的研究發表於1832年。高斯在他的《算數研究》(published 1801)中,作為處理連分數的方法提到了這個算法。約翰·狄利克雷是第一個將輾轉相除法作為數論的基礎的數學家。狄利克雷提出,數論中的很多結論,如分解的惟一性,在任何使輾轉相除法成立的數系中有效。狄利克雷的觀點被理察·戴德金修改和推廣,他用輾轉相除法研究代數整數。戴德金是第一個用高斯整數的分解惟一性證明費馬平方和定理的數學家。戴德金還率先定義了歐幾里得整環的概念。19世紀末,輾轉相除法的輝煌逐漸被戴德金的理想取代。
輾轉相除法的其他套用發展於19世紀。1829年,施圖姆將輾轉相除法用於施圖姆序列(用於確定多項式的不同實根的個數的方法)。
 19世紀最偉大的德國數學家高斯
19世紀最偉大的德國數學家高斯輾轉相除法是歷史上第一個整數關係算法(英語:integer relation algorithm),即尋找兩數的整數關係的算法。 近年來,出現了一些新穎的整數關係算法,如埃拉曼·弗格森(英語:Helaman Ferguson)和福爾卡德於1979年發表的弗格森-福爾卡德算法、以及與它相關的LLL算法(英語:Lenstra–Lenstra–Lovász lattice basis reduction algorithm)、HJLS算法以及PSLQ算法(英語:PSLQ algorithm)。
1969年,科爾(Cole)和戴維(Davie)基於輾轉相除法創造了一種二人遊戲,叫做歐幾里得遊戲。這個遊戲有最優策略。遊戲開始於兩列分別為a和b個棋子組成的序列,玩家輪流從較長一列中取走較短一列棋子數量的m倍的棋子。如果兩列棋子a和b分別由x和y個棋子組成,其中x大於y,那么玩家可以序列a的棋子數量減少為自然數x − my。最後率先將一列棋子清空的玩家勝出。
擴展歐幾里得算法
擴展歐幾里德算法:擴展歐幾里得算法(又稱擴充歐幾里得算法)是用來解某一類特定的不定方程的一種方法,常用用來求解模線性方程及方程組。擴展的歐幾里得算法可以用來計算模逆元,而模逆元在公鑰密碼學中占有舉足輕重的地位。
基本算法:對於不完全為 0 的非負整數 a,b,gcd(a,b)表示 a,b 的最大公約數,必然存在整數對 x,y ,使得 gcd(a,b)=ax+by。
證明:設 a>b。
1,顯然當 b=0,gcd(a,b)=a。此時 x=1,y=0;
2,ab≠0 時
設 ax1+by1=gcd(a,b);
bx2+(a mod b)y2=gcd(b,a mod b);
根據樸素的歐幾里德原理有 gcd(a,b)=gcd(b,a mod b);
則:ax1+by1=bx2+(a mod b)y2;
即:ax1+by1=bx2+(a-(a/b)*b)y2=ay2+bx2-(a/b)*by2;
根據恆等定理得:x1=y2; y1=x2-(a/b)*y2;
這樣我們就得到了求解 x1,y1 的方法:x1,y1 的值基於 x2,y2.
上面的思想是以遞歸定義的,因為 gcd 不斷的遞歸求解一定會有個時候 b=0,所以遞歸可以結束。
Stein算法
歐幾里德算法是計算兩個數最大公約數的傳統算法,無論從理論還是從實際效率上都是很好的。但是卻有一個致命的缺陷,這個缺陷在素數比較小的時候一般是感覺不到的,只有在大素數時才會顯現出來。
Stein算法由J. Stein 1961年提出,這個方法也是計算兩個數的最大公約數。和歐幾里德算法算法不同的是,Stein算法只有整數的移位和加減法,這對於程式設計者是一個福音。
Stein算法:
1、如果A=0,B是最大公約數,算法結束
2、如果B=0,A是最大公約數,算法結束
3、設定A1=A、B1=B和C1=1
4、如果An和Bn都是偶數,則An+1=An/2,Bn+1=Bn/2,Cn+1=Cn*2(注意,乘2隻要把整數左移一位即可,除2隻要把整數右移一位即可)
5、如果An是偶數,Bn不是偶數,則An+1=An/2,Bn+1=Bn,Cn+1=Cn (很顯然啦,2不是奇數的約數)
6、如果Bn是偶數,An不是偶數,則Bn+1=Bn/2,An+1=An,Cn+1=Cn (很顯然啦,2不是奇數的約數)
7、如果An和Bn都不是偶數,則An+1=|An-Bn|,Bn+1=min(An,Bn),Cn+1=Cn
8、n加1,轉1 考慮歐幾里德算法,最惡劣的情況是,每次疊代a=2b-1,這樣,疊代後,r=b-1。如果a小於2N,這樣大約需要4N次疊代。而考慮Stein算法,每次疊代後,顯然A(n+1)B(n+1)≤AnBn/2,最大疊代次數也不超過4N次。也就是說,疊代次數幾乎是相等的。但是,需要注意的是,對於大素數,試商法將使每次疊代都更複雜,因此對於大素數Stein將更有優勢。
基本介紹
 最大公約數
最大公約數最大公約數(greatest common divisor,簡寫為gcd;或highest common factor,簡寫為hcf),指某幾個整數共有因子中最大的一個。
能夠整除一個整數的整數稱為其的約數(如5是10約數);
能夠被一個整數整除的整數稱為其的倍數(如10是5的倍數);
如果一個數既是數A的約數,又是數B的約數,稱為A,B的公約數,A,B的公約數
中最大的一個(可以包括AB自身)稱為AB的最大公約數
定義
如果有一個自然數a能被自然數b整除,則稱a為b的倍數,b為a的約數。幾個自然數公有的約數,叫做這幾個自然數的公約數。公約數中最大的一個公約數,稱為這幾個自然數的最大公約數。
例: 在2、4、6中,2就是2,4,6的最大公約數。
早在公元前300年左右,歐幾里得就在他的著作《幾何原本》中給出了高效的解法——輾轉相除法。輾轉相除法使用到的原理很聰明也很簡單,假設用f(x, y)表示x,y的最大公約數,取k = x/y,b = x%y,則x = ky + b,如果一個數能夠同時整除x和y,則必能同時整除b和y;而能夠同時整除b和y的數也必能同時整除x和y,即x和y的公約數與b和y的公約數是相同的,其最大公約數也是相同的,則有f(x, y)= f(y, x%y)(y > 0),如此便可把原問題轉化為求兩個更小數的最大公約數,直到其中一個數為0,剩下的另外一個數就是兩者最大的公約數。
例如,12和30的公約數有:1、2、3、6,其中6就是12和30的最大公約數。
輾轉相除法是古希臘求兩個正整數的最大公約數的,也叫歐幾里德算法,其方法是用較大的數除以較小的數,上面較小的除數和得出的餘數構成新的一對數,繼續做上面的除法,直到出現能夠整除的兩個數,其中較小的數(即除數)就是最大公約數。以求288和123的最大公約數為例,操作如下:
288÷123=2餘42
123÷42=2餘39
42÷39=1餘3
39÷3=13
所以3就是288和123的最大公約數。
性質
重要性質:gcd(a,b)=gcd(b,a) (交換律)
gcd(-a,b)=gcd(a,b)
gcd(a,a)=|a|
gcd(a,0)=|a|
gcd(a,1)=1
gcd(a,b)=gcd(b, a mod b)
gcd(a,b)=gcd(b, a-b)
如果有附加的一個自然數m,
則: gcd(ma,mb)=m * gcd(a,b) (分配律)
gcd(a+mb ,b)=gcd(a,b)
如果m是a和b的最大公約數,
則: gcd(a/m ,b/m)=gcd(a,b)/m
在乘法函式中有:
gcd(ab,m)=gcd(a,m) * gcd(b,m)
兩個整數的最大公約數主要有兩種尋找方法:
* 兩數各分解質因數,然後取出同樣有的質因數乘起來
*輾轉相除法(擴展版)
和最低公倍數(lcm)的關係:
gcd(a, b) * lcm(a, b) = ab
a與b有最大公約數,
兩個整數的最大公因子可用於計算兩數的最低公倍數,或分數化簡成最簡分數。
兩個整數的最大公因子和最低公倍數中存在分配律:
* gcd(a, lcm(b, c)) = lcm(gcd(a, b), gcd(a, c))
* lcm(a, gcd(b, c)) = gcd(lcm(a, b), lcm(a, c))
 最大公約數
最大公約數 最大公約數
最大公約數在坐標里,將點(0, 0)和(a, b)連起來,通過整數坐標的點的數目(除了(0, 0)一點之外)就是gcd(a, b)。
套用貝祖
注意:網頁中無法顯示數學中的腳標! a0,a1,...,a(n-1),a(n) 是數列,r1.r2,...,r(n-1),r(n)也是數列。 r(n-1) 即數列的第(n-1)項 別弄錯了。
對任意兩個整數a、b,設d是它們的最大公約數。那么關於未知數x和y的線性丟番圖方程(稱為貝祖等式):
貝祖等式,依艾蒂·貝祖命名,是線性丟番圖方程。它說明若有整數a、b和其最大公因子d,必存在整數x、y使得: ax + by = d x、y稱為貝祖數,可用擴展版輾轉相除法求得,但結果不是唯一的。
例如12和42的最大公因子是6,便可以寫(-3)×12 + 1×42 = 6及4×12 + (-1)×42 = 6。 d其實就是最小可以寫成ax + by形式的正整數。
輾轉相除法是用來求最大公約數的.我們用代數的形式來表達(實質上,算術形式也是可以完全講得清楚的).
給出兩個正整數a和b,用b除a得商a0,餘數r,寫成式子 a=a0b+r,0≤r
(1) 這是最基本的式子,輾轉相除法的靈魂.如果r等於0,那么b可以除盡a,而a、b的最大公約數就是b. 如果r≠0,再用r除b,得商a1,餘數r1,即 b=a1r+r1,0≤r1
(2) 如果r1=0,那么r除盡b,由(1)也除盡a,所以r是a、b的公約數.反之,任何一除盡b的數,由(1),也除盡r,因此r是a、b的最大公約數. 如果r1≠0,則用r1除r得商a2,餘數r2,即 r=a2r1+r2,0≤r2
(3) 如果r2=0,那么由(2)可知r1是b、r的公約數,由(1),r1也是a、b的公約數.反之,如果一數除得盡a、b,那末由(1),它一定也除得盡b、r,由(2),它一定除得盡r、r1,所以r1是a、b的最大公約數. 如果r2≠0,再用r2除r1,如法進行.由於b>r>r1>r2>…逐步小下來,而又都是正整數,因此經過有限步驟後一定可以找到a、b的最大公約數d(它可能是1).這就是有名的輾轉相除法,在外國稱為歐幾里得算法.
這個方法不但給出了求最大公約數的方法,而且幫助我們找出x、y,使 ax+by=d.
(4)在說明一般道理之前,先看下面的例子. 從求42897與18644的最大公約數出發: 42897=2×18644+5609, (i) 18644=3×5609+1817, (ii) 5609=3×1817+158, (iii) 1817=11×158+79, (iv) 158=2×79. 這樣求出最大公約數是79.
我們現在來尋求x、y,使 42897x+18644y=79. 由(iv)可知 1817-11×158=79. 把(iii)式的158表達式代入此式,得 79=1817-11(5609-3×1817) =34×1817-11×5609. 再以(ii)式的1817表達式代入,得 79=34×(18644-3×5609)-11×5609 =34×18644-113×5609. 再以(i)式的5609表達式代入,得 79=34×18644-113×(42897-2×18644) =260×18644-113×42897. 也就是x=-113,y=260. 這雖然是特例,也說明了一般的理論.
一般的理論是:把輾轉相除法寫成為 a=a0b+r, b=a1r+r1, r=a2r1+r2, r1=a3r2+r3, ……… r(n-1)=a(n+1)r(n)+ r(n+1), r(n)=a(n+2)r(n+1). 這樣得出最大公約數d=r(n+1).由倒數第二式,r(n+1)可以表為r(n-1)、r(n)的一次式,再倒回一個可以表為r(n-2)、r(n-1)的一次式,…,最後表為a、b的一次式.即把d放在等式的一邊,另一邊不斷代入上一個等式,最後可找出一組(x、y)值,使 ax+by=d. 成立。由此,貝式等式得證。
