釋義
 15和25的公因
15和25的公因公約數與公倍數相反,就是既是A的約數同時也是B的約數的數,12和15的公約數有1,3,最大公約數就是3。再舉個例子,30和40,它們的公約數有1,2,5,10,最大公約數是10。
公因數,又稱公約數。在數論的敘述中,如果n和d都是整數,而且存在某個整數c,使得n=cd,就說d是n的一個因數,或說n是d的一個倍數,記作d|n(讀作d整除n)。如果d|a且d|b,我們就稱d是a和b的一個公因數。根據裴蜀定理,對每一對整數a,b,都有一個公因數d,使得d=ax+by,其中x和y是某些整數,並且a和b的每一個公因數都能整除這個d。於是d的絕對值叫做最大公因數。
求幾個整數的最大公因數,只要把它們的所有共有的質因數連乘,所得的積就是它們的最大公因數。
最大公因數
定義
如果數a能被數b整除,a就叫做b的倍數,b就叫做a的約數。約數和倍數都表示一個整數與另一個整數的關係,不能單獨存在。如只能說16是某數的倍數,2是某數的約數,而不能孤立地說16是倍數,2是約數。"倍"與"倍數"是不同的兩個概念,"倍"是指兩個數相除的商,它可以是整數、小數或者分數。"倍數"只是在數的整除的範圍內,相對於"約數"而言的一個數字的概念,表示的是能被某一個自然數整除的數。
幾個整數,公有的約數,叫做這幾個數的公約數;其中最大的一個,叫做這幾個數的最大公約數。例如:12、16的公約數有1、2、4,其中最大的一個是4,4是12與16的最大公約數,一般記為(12,16)=4。12、15、18的最大公約數是3,記為(12,15,18)=3。
幾個自然數公有的倍數,叫做這幾個數的公倍數,其中最小的一個自然數,叫做這幾個數的最低公倍數。例如:4的倍數有4、8、12、16,……,6的倍數有6、12、18、24,……,4和6的公倍數有12、24,……,其中最小的是12,一般記為[4,6]=12。12、15、18的最低公倍數是180。記為[12,15,18]=180。若干個互質數的最低公倍數為它們的乘積的絕對值。
求法
質因數分解法把幾個數先分別分解質因數,再把各數中的全部公有的質因數和獨有的質因數提取出來連乘,所得的積就是這幾個數的最低公倍數。
例如:求6和15的最低公倍數。先分解質因數,得6=2×3,15=3×5,6和15的全部公有的質因數是3,6獨有質因數是2,15獨有的質因數是5,2×3×5=30,30裡面包含6的全部質因數2和3,還包含了15的全部質因數3和5,且30是6和15的公倍數中最小的一個,所以[6,15]=30。
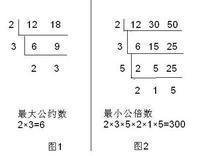
短除法
短除法:短除法求最大公約數,先用這幾個數的公約數連續去除,一直除到所有的商互質為止,然後把所有的除數連乘起來,所得的積就是這幾個數的最大公約數。短除法的本質就是質因數分解法,只是將質因數分解用短除符號來進行。
短除符號就是除號倒過來。短除就是在除法中寫除數的地方寫兩個數共有的質因數,然後落下兩個數被公有質因數整除的商,之後再除,以此類推,直到結果互質為止(兩個數互質)。
而在用短除計算多個數時,對其中任意兩個數存在的因數都要算出,其它沒有這個因數的數則原樣落下。直到剩下每兩個都是互質關係。求最大公因數便乘一邊,求最低公倍數便乘一圈。無論是短除法,還是分解質因數法,在質因數較大時,都會覺得困難。這時就需要用新的方法。
輾轉相除法
輾轉相除法:輾轉相除法是求兩個自然數的最大公約數的一種方法,也叫歐幾里德算法。
這就是輾轉相除法的原理。
例如,求(319,377):
∵319÷377=0(餘319)
∴(319,377)=(377,319);
∵377÷319=1(餘58)
∴(377,319)=(319,58);
∵319÷58=5(餘29)
∴(319,58)=(58,29);
∵58÷29=2(餘0)
∴(58,29)=29;
∴(319,377)=29。
可以寫成右邊的格式。
用輾轉相除法求幾個數的最大公約數,可以先求出其中任意兩個數的最大公約數,再求這個最大公約數與第三個數的最大公約數,依次求下去,直到最後一個數為止。最後所得的那個最大公約數,就是所有這些數的最大公約數 。
套用
一般題目
試卷上會讓你去求某若干個數的最大公因數。例:
12和18的最大公因數
12的因數有:±1、±2、±3、±4、±6、±12
18的因數有:±1、±2、±3、±6、±9、±18
12和18的公因數有:±1、±2、±3、±6,而最大的數是6,最大公因數也就是6了!
計算方法
1.倍數關係若較大數是較小數的倍數,那么較小數是這兩個數的最大公因數。
2.互質關係
公因數只有±1的兩個數,叫互質數。例如,5和7是互質數。
註:1是任何整數的因數。
題目只會讓你求最大公因數,最小必定是1(0與負數除外)