簡介
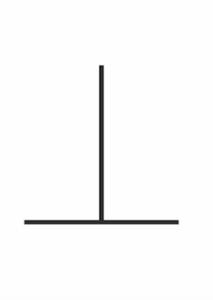
 直角
直角 在幾何學和三角學中,直角,又稱正角,是角度為90度的角。它相對於四分之一個圓周(即四分之一個圓形),而兩個直角便等於一個半角(180°)。角度比直角小的稱為銳角,比直角大而比平角小的稱為鈍角。一個直角等於90度,符號:Rt∠。
角度
兩條相交直線中的任何一條與另一條相疊合時必須轉動的量的量度,轉動在這兩條直線的所在平面上並繞交點進行。
角度是用以量度角的單位,符號為°。一周角分為360等份,每份定義為1度(1°)。
採用360這數字,因為它容易被整除。360除了1和自己,還有22個真因數,包括了7以外從2到10的數字,所以很多特殊的角的角度都是整數。
實際套用中,整數的角度已足夠準確。有時需要更準確的量度,如天文學或地球的經度和緯度,除了用小數表示度,還可以把度細分為分和秒:1度為60分(60′),1分為60秒(60″)。例如40.1875° = 40°11′15″。要更準確便用小數表示秒,而不再加設單位。
直角也就是90度的角。
教學設計
教學內容:直角的初步認識。
教學要求:
1、使學生初步認識直角,並能拿握直角的特徵;
2、培養學生的初步判斷能力,讓學生學會用三角板判斷直角和畫直角;
3、通過動手操作,促進學生空間觀念的發展。
教會判斷的方法:
教師演示並說明判斷的方法:先將三角板上的直角的頂點和角的頂點合在一起,再將三角板上直角的一條邊跟角的一條邊重合在一起,看看三角板直角的另一條邊和角的另一條邊是不是重合在一起;如果不重合在一起,這個角就不是直角;如果重合在一起,這個角就是直角。
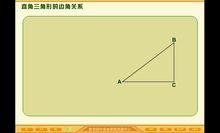
直角三角形
直角三角形是一個幾何圖形,是有一個角為直角的三角形,有普通的直角三角形和等腰直角三角形兩種。其符合勾股定理,具有一些特殊性質和判定方法。
它除了具有一般三角形的性質外,具有一些特殊的性質:
1、直角三角形兩直角邊的平方和等於斜邊的平方。如圖,∠BAC=90°,則AB²+AC²=BC²(勾股定理)
2、在直角三角形中,兩個銳角互余。如圖,若∠BAC=90°,則∠B+∠C=90°
3、直角三角形中,斜邊上的中線等於斜邊的一半(即直角三角形的外心位於斜邊的中點,外接圓半徑R=C/2)。該性質稱為直角三角形斜邊中線定理。
4、直角三角形的兩直角邊的乘積等於斜邊與斜邊上高的乘積。
解直角三角形這一部分知識看似方法多樣,讓人眼花繚亂,其實萬變不離其中,知識的結構是十分嚴謹的。在心理認知過程中,教師要重點加強學生的認知培養,要讓學生能自我體驗、自我觀察和自我調節。這有利於學生學習自覺能動性的提高和學生自學能力的提高,學生的智力也得到了提高,這是解決學生如何學習的行之有效的方法和途徑。對於學生的個性品質,教師要認真貫徹教學大綱的相關要求,重點在於培養學生的學習興趣和良好的學習習慣,要能夠針對學生的個性差異“因材施教”,讓學生在學習的過程中樹立正確的信念和三觀,並養成良好的學習習慣和性格品質。課堂教學是中學生心理教育的主要渠道。教師在備課的時候就要充分挖掘學生的心理,展開各種形式的講座和小組活動,並及時地對學生進行心理健康教育和心理疏導。在學校里,要形成良好的校風和管理制度;班級中要能夠形成良好的班風和班級文化;社會要能夠擴大改革力度,形成良好的人才選拔機制和學校建設,要能夠大力宣傳素質教學的重要性。作為家長,要形成正確的子女成才觀,要能夠為子女創設良好的家庭氛圍。根據孩子的個性特點順其自然地引導子女的健康發展。在這樣的環境中,學生才能夠感受到自己的用武之地,才能夠養成良好的學習習慣,培養自己的數學素質,促進自己的全面發展。