定義
群中元素可以由最小數目個群元的乘積生成,這組群元稱為該群的生成元,生成元的數目為有限群的秩。
例如 D3 群,D3={E,D,F,A,B,C},其中 E 為恆元, D、F 為繞等邊三角形中點逆時針旋轉 2π/3 和 4π/3 ,A,B,C 為繞三個對稱軸的翻轉。其中,可取生成元為 {D,A} ,E=D³=A²,F=D²,B=AD,C=DA;也可取生成元為{F,A},E=F³=A²,D=F²,B=FA,C=AF。
秩:生成元的數目為有限群的秩。有限群的生成元的選擇不唯一,但秩不變。
生成子群
設S是群G的一個非空子集,令M是G中所有包含S的子群所組成的集合,即M={H<G|S⊆H}。G顯然包含S,所以G∈M,從而M非空。令K=∩H,H∈M,則K是G的子群。稱K為群G的由子集S所生成的子群,簡稱生成子群,記作〈S〉,即K=〈S〉=∩H,S⊆H<G。子集S稱為〈S〉的生成元組。
自由李代數
[free Lie algebra]
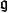 生成元
生成元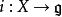 生成元
生成元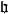 生成元
生成元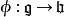 生成元
生成元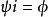 生成元
生成元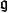 生成元
生成元設 X 為非空集合。若域 K 上的李代數 帶有一個單射 ,使得對於任何 K 李代數 及映射 ,使得 ,則稱 是 X 上的一個自由李代數。
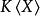 生成元
生成元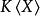 生成元
生成元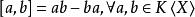 生成元
生成元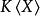 生成元
生成元在同構意義下,非集合 X 上的自由李代數存在且唯一。事實上,設 為 X 上的自由結合代數,於是 關於括弧積 做成一個李代數。此李代數的由 X 生成的李子代數即為 X 上的一個自由李代數,而 為其泛包絡代數。
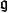 生成元
生成元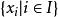 生成元
生成元 生成元
生成元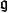 生成元
生成元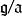 生成元
生成元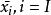 生成元
生成元若 為 上的一個自由李代數, 為 的由 生成的理想。則稱 為生成元,為 ,關係(relation)為 的李代數。

