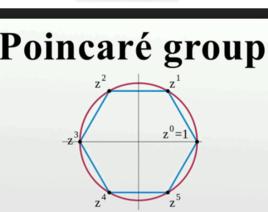
基本解釋
等距同構是一種事物在事件間的時空軌跡上的移動方式,而這樣做是不會影響原時的。例如,所有事件被延後了兩小時,而這兩小時中包括了兩項事件,以及你從事件一到事件二的路徑,那么你的計時器所量度出的,兩事件間的時間間距會是一樣的。又例如,所有事物被移到西邊五公里外的地方,那么你所量度出的時間間距也不會改變。而這種移動的結果是不會影響棍子長度的。
如果我們無視重力效應的話,那么一共有十種移動方式:在時間上的平移,在三維空間中任一維上的平移,在三條空間軸上任一條的(定角)旋轉,或三維任一方向上的直線性洛倫茲變換,因此是1 + 3 + 3 + 3 = 10。
如果將這種等距同構結合起來(即執行一個之後再執行另一個),那么所得的結果也會是等距同構(然而,這一般來說只限於上述十種基本移動之間的線性組合)。這些等距同構因此形成了一個群。也就是說,它們當中存在單位元(即不移動,停留在原先的地方)及逆元(將事物移動回原先的位置),同時亦遵守結合律。這種特定群的名字叫做“ 龐加萊群”。
在古典物理學中,對應龐加萊群的群叫伽利略群,也是有十個生成元的,伽利略群作用於絕對時空。而在伽利略群中取代直線性洛倫茲變換的是,聯繫兩個共動慣性參考系的錯切變換。
專門解釋
龐加萊群是閔可夫斯基時空的等距同構群。它是一種十維的非緊李群。平移的阿貝爾群是一個正規子群,而洛倫茲群也是一個子群,原點的穩定子群。龐加萊群本身是仿射群的最小子群,而仿射群就包括了所有的變換與洛倫茲變換。準確一點來說,龐加萊群是平移群與洛倫茲群的半直積
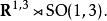 龐加萊群
龐加萊群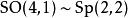 龐加萊群
龐加萊群另一種解釋方式是,把龐加萊群視為洛倫茲群的群擴張,而擴張的部分則是它的矢量群表示;因此龐加萊群有一個不正式的稱呼,叫“非均勻洛倫茲群”(inhomogeneous Lorentz group)。另外,當德西特半徑趨向無限大時,德西特群(de Sitter group) 的群收縮就是龐加萊群。
它的正能量么正不可約表示是由質量(非負數)與自旋(整數或半整數)所標記的,並與量子力學的粒子有關。
與愛爾蘭根綱領一致,閔可夫斯基空間的幾何由龐加萊群所規定的:閔可夫斯基空間可被視為龐加萊群的齊性空間。
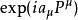 龐加萊群
龐加萊群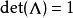 龐加萊群
龐加萊群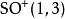 龐加萊群
龐加萊群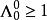 龐加萊群
龐加萊群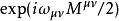 龐加萊群
龐加萊群龐加萊代數是龐加萊群的李代數。更具體的來說,正式的( ),也就是洛倫茲子群(它的單位連通區) 的正確時間( )部分,是與單位元有關係的,因此可用矩陣指數與 表示。在分量形式中,龐加萊群可用以下的交換關係表示:
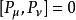 龐加萊群 龐加萊群 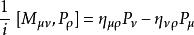 龐加萊群 龐加萊群 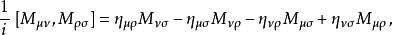 龐加萊群 龐加萊群 |
其中P為平移生成元,M為洛倫茲變換生成元,η為閔可夫斯基度規。
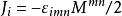 龐加萊群
龐加萊群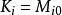 龐加萊群
龐加萊群以下的是與(均勻)洛倫茲群的交換關係,洛倫茲群由旋轉( )及直線性洛倫茲變換( )所組成。在這樣的標記下,可以用非協變形式(但較實用)來表示整個龐加萊代數
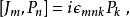 龐加萊群
龐加萊群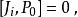 龐加萊群
龐加萊群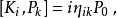 龐加萊群
龐加萊群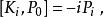 龐加萊群
龐加萊群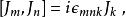 龐加萊群
龐加萊群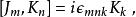 龐加萊群
龐加萊群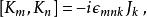 龐加萊群
龐加萊群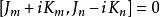 龐加萊群
龐加萊群其中最下面的是兩個直線性洛倫茲變換的交換關係,很多時候會被稱作“維格納旋轉”。注意根據上述關係, ,這是一項重要的簡化,能使洛倫茲子代數約化至 su(2)⊕ su(2),並且使應付洛倫茲群的表示論的方法有效得多。
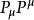 龐加萊群
龐加萊群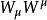 龐加萊群
龐加萊群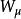 龐加萊群
龐加萊群這種代數的卡西米爾不變數為 與 ,其中 為泡利-魯班斯基假矢量;它們的作用是標記群表示。
龐加萊群是任何相對論性量子場的完全對稱群。因此,所有基本粒子都能成為這個群表示的一部分。這些表示一般是由兩種物件所指明的:每一粒子的四維動量平方(即質量平方),和內稟量子數{\displaystyle J^{PC}},其中J為自旋量子數,P為宇稱,C為電荷共軛量子數。實際上許多量子場會破壞宇稱與電荷共軛。在那些情況下就會棄用被破壞的P和C。由於每一套量子場論均需擁有CPT不變性,因此要從P和C構建時間反轉量子數T是件很容易的事。
作為拓撲空間,這個群共有四個連通區:單位區、時間反轉區、空間顛倒區、以及同時出現時間反轉與空間顛倒的區。
龐加萊對稱
龐加萊對稱是狹義相對論的完全對稱,當中包括:
•在時間與空間中的平移(即位移),P。它們形成了描述時空中的平移的阿貝爾李群。
•空間中的旋轉(它們形成了描述三維旋轉的非阿貝爾李群,其生成元為J)
•直線性洛倫茲變換,即聯繫兩個均勻移動物體的變換,其生成元為K。
上述最後兩種對稱, J及 K,組合起來就成了洛倫茲群(見洛倫茲不變性)。
它們都是一種叫 龐加萊群的李群的生成元,而龐加萊群是平移群與洛倫茲群的半直積。在這個群下不變的物件,可被稱為擁有 龐加萊不變性或 相對論性不變性。