跨聲速流數值計算

跨聲速流的主要特點就是既有亞聲速又有超聲速的混合流場。以高亞聲速機翼繞流為例，亞聲速流場占據著外流場的絕大部分，只是在機翼表面附近有小塊的超聲速流場，並可能出現激波。

正文

　如果激波不太強，則整個無粘流場可以用等熵無旋流來外理。這種流動具有速度勢函式， 速度分量便是勢函式的方嚮導數。 描述這種流場的基本運動方程是空氣動力學中常用的速度勢方程。當流場中的速度偏離聲速不太遠，還可以用小擾動理論將速度勢方程進行簡化。二維定常流動的小擾動方程是：　

，

式中為擾動速度勢函式,的下標表示偏微商。這個方程既是非線性的(因為馬赫數是速度的函式),又是混合型的。在超聲速區(＞1)，它和波動方程一樣屬於雙曲型；在亞聲速區(＜1)，它又類似拉普拉斯方程，屬橢圓型。解跨聲速位勢流的方法主要有下面幾種：
速度圖法　此法為蘇聯學者С.А.恰普雷金於1905年提出。它的實質是把定義於物理平面(x，y)上的方程，通過嚴格的數學變換轉換到速度平面(u，v)上，使變換後的方程在速度平面上是線性的。這樣就可用疊加法來求解速度勢函式。然後再把結果反演到物理平面上，從而得到物理平面上的解。對從物面上的已知壓力分布來求物面形狀的這類問題，速度圖法特別有用，但它不能用來計算含有激波的流動，而且也不能推廣到三維流動。
混合差分法　跨聲速流數值計算的一個常用方法是有限差分方法，此法將微分方程離散化，變成差分方程，在一定的初邊值條件下直接求解，但在定常流動中，亞聲速區和超聲速區擾動傳播規律不同。在亞聲速區，擾動向四周相鄰區傳播，而在超聲速區，擾動只向下游影響區傳播。影響區是以擾動源為頂點的後向馬赫錐。E.M.穆曼和J.D.科爾針對這種流場的特點，採用了混合差分格式。在亞聲速區用中心差分，因為所有鄰近網點上的參數值都會影響計算點,這也是橢圓型方程的特點,在超聲速區則用迎風格式，因為上游迎風網點正好是雙曲型波動方程的依賴區,也就是前向馬赫錐(圖1)。對薄物體繞流來說,流線方向基本沿著x軸,所以只要對x 的偏導數用混合差分格式即可(圖2)。對鈍體繞流來說,流場中各點的流線方向偏離x軸很大，因而須旋轉坐標軸，使x軸與當地流線方向一致,然後對x的導數用混合差分。A.詹姆森正是用這種方法改進了原來的混合差分格式，稱為“旋轉差分法”，此法能提高計算精度，但計算工作量也隨之增加。

時間相關法　時間相關法實際上是把一個定常繞流問題，看作是一個非定常繞流問題在時間趨向無窮時的穩定解。非定常無粘流動的基本方程是：

，

式中u、v是速度在x、y方向上的分量；E為能量；p為壓強；ρ為密度;t為時間。下標t、x、y表示對它們的偏微商。上式代表四個偏微分方程，它們的變數是ρ、u、v和E，也可用ρ、ρu、ρv和ρE這四個變數表示,視計算時的方便而定。第一個偏微分方程是ρt+(ρu)x+(ρv)y=0，余類推。無論是超聲速流動還是亞聲速流動，這組方程總是雙曲型的，都可用相同的差分格式。但這組方程已有成熟的解法。R.馬格納斯和H.姚希哈娜利用差分方程的數值粘性自動“捕捉”激波，G.莫雷蒂利用完全守恆型格式來處理激波，他們都成功地進行了定常跨聲速流動的計算。
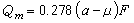時間相關法能計算含有強激波的有旋流，但所需的計算時間很長，往往是混合差分法的數倍。跨聲速流計算今後的任務主要在於提高對複雜組合體計算的精度和計算效率。
參考書目
　G.Y.Nieuwland and B. M.Spee,Transonic Airfoils,Recent Developments　in　Theory, Experiment　and Design,Annual　Review　of Fluid Mechanics,Vol.5,1973.
　羅時鈞、鄭郁文、雪蝶茜、錢鴻編著：《跨聲速定常勢流的混合差分法》，國防工業出版社，北京，1979。

配圖

相關連線