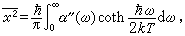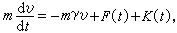漲落耗散定理
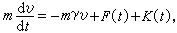
漲落耗散定理是聯繫不可逆過程中能量耗散和熱平衡狀態熱漲落的重要定理。
漲落耗散定理
正文
聯繫不可逆過程中能量耗散和熱平衡狀態熱漲落的重要定理。
外力場中小粒子的布朗運動,遵從朗之萬方程 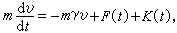
式中m是布朗粒子的質量, v是速度,γ是阻力係數,右邊的第一、第二和第三項分別表示布朗粒子所受到的摩擦力、漲落力和外力。20世紀初,A.愛因斯坦在研究布朗運動時,就揭示了擴散係數D和遷移率μ之間的關係D=μ k T。另外,漲落力F(t)的譜密度同摩擦係數mγ和k T成正比。這反映了摩擦的能量耗散機構和熱平衡狀態下的漲落密切相關。
朗之萬方程式可推廣為下述形式 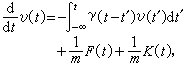 (1)
(1)
式中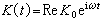 是時間的周期函式,摩擦阻力由粒子瞬時速度決定,但有滯後效應,γ(t)為滯後阻力函式。
是時間的周期函式,摩擦阻力由粒子瞬時速度決定,但有滯後效應,γ(t)為滯後阻力函式。
布朗粒子受到外力作用時,感應的平均速度是 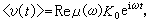
這裡μ(ω)是同頻率ω對應的複數遷移率。若對式(1)取平均,注意到漲落力平均值為零,即〈F(t)〉=0,那么容易得到 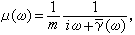 (2)
(2)
式中 孻(ω)是 γ(t)的傅立葉-拉普拉斯變換,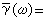
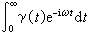 。外力K為零時,用複變函數理論可以導出
。外力K為零時,用複變函數理論可以導出 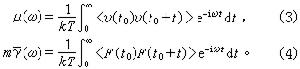
其中〈υ(t0)v(t0+t)〉和<F(t0)F(t0+t)>分別是速度相關函式和漲落力相關函式。這兩個公式稱為漲落耗散定理。式(3)和給出複數遷移率(又稱導納)同速度(一般是流)相關函式之間的關係,前者作為後者的傅立葉-拉普拉斯變換,又稱第一漲落耗散定理。由它可以得出愛因斯坦關係,可見,愛因斯坦關係恰好是第一漲落耗散定理的特殊情形。式 (4)給出複數阻力係數(一般是阻抗)作為漲落力F(t)的相關函式的傅立葉-拉普拉斯變換,又稱第二漲落耗散定理。第一、第二漲落耗散定理表明,遷移率和阻力係數這些代表系統對外力的回響的量和平衡系統沒有外力作用時所具有的熱漲落密切相關。因為對外界的回響包含能量的耗散部分,故漲落耗散定理由此得名。
導體中作熱運動的電子(也是一種布朗運動)在電場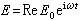 作用下,產生熱漲落電流密度為
作用下,產生熱漲落電流密度為 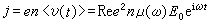 ,
,
則複數電導率為 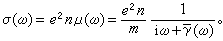
對應的漲落耗散定理具有如下形式 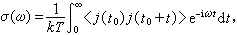
若σ(ω)同ω無關,則有 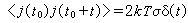 。
。
當橫截面為S,長度為L的導電棒處於溫度T時,由於電子熱運動漲落,棒兩端熱漲落的電壓為V(t)=S j(t)R,式中R為電阻。根據上式,可得漲落電壓的相關函式為 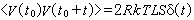 ,
,
對於單位體積,應有 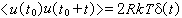 ,
,
若取u(t)的傅立葉分量,則上式又可寫為 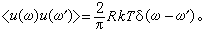
這就是著名的尼奎斯特方程。它首先由H.尼奎斯特給出,它和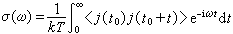 等價。在建立漲落耗散定理方面,許多學者如H.B.卡倫,T.A.韋爾頓和久保亮五等都作出了貢獻。
等價。在建立漲落耗散定理方面,許多學者如H.B.卡倫,T.A.韋爾頓和久保亮五等都作出了貢獻。
廣義地說,即使是非熱力學的漲落行為,也可以同外力對系統的作用聯繫起來。即不論是經典的,還是具有量子性質的物理量,漲落耗散定理都成立。設憫為同某物理量對應的量子力學算符,K(t)是和時間有關的“微擾力”,則外界對系統的微擾哈密頓算符是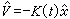 ,在這種情況下,量子力學的平均值塣不等於零,應是
,在這種情況下,量子力學的平均值塣不等於零,應是 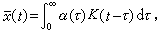
式中α(τ)是同媒質性質有關的時間函式,它描述系統對外力的回響,又稱為回響函式。塣在某一時間t的值,當然只依賴於力K(t)在此時以前各個時刻的值,故塣(t)取上述形式。利用傅立葉變換, 塣和K的關係式塣=α(ω)K中的α(ω)是α(τ)的傅立葉係數,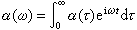 。α(ω)稱為廣義感應率。 如果知道了α(ω),則系統在這種擾動下的行為就完全確定了。一般說來 α(ω) 取複數的形式α(ω)=α┡(ω)+iα″(ω)。若設K(t)是簡正函式,它取如下的實數表示
。α(ω)稱為廣義感應率。 如果知道了α(ω),則系統在這種擾動下的行為就完全確定了。一般說來 α(ω) 取複數的形式α(ω)=α┡(ω)+iα″(ω)。若設K(t)是簡正函式,它取如下的實數表示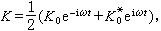 則可以求得來源於外界擾動的單位時間內的能量耗散為
則可以求得來源於外界擾動的單位時間內的能量耗散為 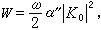
式中感應率的虛部α″可以表示成 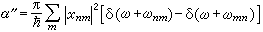 ,
,
其中x nm是算符憫的矩陣元。可見,能量耗散決定於感應率的虛部。
卡倫和韋爾頓1951年證明了一個重要關係式 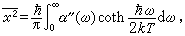
這關係是漲落耗散定理最一般的形式,當平衡系統受到迫使其離開平衡狀態的外力作用時,這一關係把物理量的漲落和可能實現的耗散過程聯繫了起來。從分析平衡態系統的熱漲落,可以求得系統的輸運性質。
參考書目
戶田盛和、久保亮五編:《統計物理學》,岩波,東京,1978。
Л.Д.朗道、Ε.М.栗弗席茲著,楊訓愷等譯:《統計物理學》,高等教育出版社,北京,1965。配圖
相關連線
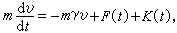
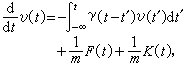 (1)
(1)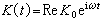 是時間的周期函式,摩擦阻力由粒子瞬時速度決定,但有滯後效應,γ(t)為滯後阻力函式。
是時間的周期函式,摩擦阻力由粒子瞬時速度決定,但有滯後效應,γ(t)為滯後阻力函式。 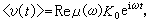
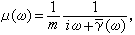 (2)
(2)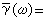
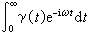 。外力K為零時,用複變函數理論可以導出
。外力K為零時,用複變函數理論可以導出 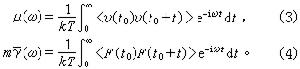
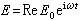 作用下,產生熱漲落電流密度為
作用下,產生熱漲落電流密度為 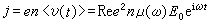 ,
,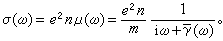
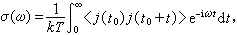
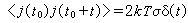 。
。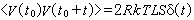 ,
,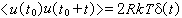 ,
,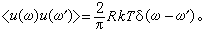
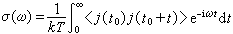 等價。在建立漲落耗散定理方面,許多學者如H.B.卡倫,T.A.韋爾頓和久保亮五等都作出了貢獻。
等價。在建立漲落耗散定理方面,許多學者如H.B.卡倫,T.A.韋爾頓和久保亮五等都作出了貢獻。 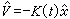 ,在這種情況下,量子力學的平均值塣不等於零,應是
,在這種情況下,量子力學的平均值塣不等於零,應是 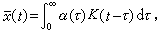
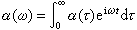 。α(ω)稱為廣義感應率。 如果知道了α(ω),則系統在這種擾動下的行為就完全確定了。一般說來 α(ω) 取複數的形式α(ω)=α┡(ω)+iα″(ω)。若設K(t)是簡正函式,它取如下的實數表示
。α(ω)稱為廣義感應率。 如果知道了α(ω),則系統在這種擾動下的行為就完全確定了。一般說來 α(ω) 取複數的形式α(ω)=α┡(ω)+iα″(ω)。若設K(t)是簡正函式,它取如下的實數表示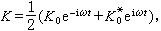 則可以求得來源於外界擾動的單位時間內的能量耗散為
則可以求得來源於外界擾動的單位時間內的能量耗散為 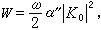
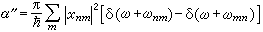 ,
,