概念
準素理想(primary ideal)是一種特殊的理想。理想論中理想分解的基礎。設Q是交換環R的理想且Q≠R,如果對R中任意元素x,y,xy∈Q且x∉Q,恆有正整數n,使得y∈Q,則稱Q是R的準素理想。素理想是準素理想,但素理想的冪未必是準素理想。
理想
理想是集合論中的基本概念之一。設S為任意集合,若I⊆P(S)且滿足:
1.∅∈I;
2.若X,Y∈I,則X∪Y∈I;
3.若X,Y⊆S,X∈I,Y⊆X,則Y∈I;
則稱I為集合S上的理想。理想的概念在現代數學的幾乎每個分支中均有套用,且有許多變體或引申。例如,布爾代數上的理想即為集合上的理想的一種變體。設B為任意布爾代數,若B的一個子集I滿足:
1.0∈I,1∉I(其中0,1分別為布爾代數B中的零元與么元);
2.對任何u∈I,v∈I,有u+v∈I;
3.對任何u,v∈B,若u∈I且v≤u,又v∈I;
則稱I為B上的理想。
理想論
理想論是與環的理想密切相關的理論。它是交換環理論的重要部分。20世紀20年代初,由諾特(Noether,E.)所建立的一般交換環上理想的準素分解理論與20世紀30年代克魯爾(Krull,W.)的局部環與維數理論。這一理論使古典幾何建立在堅實的代數基礎之上,形成了代數幾何這門學科.理想論也是代數數論的重要工具。
素理想
素理想是一類特殊理想。它是整數環中素數生成理想的推廣。設P是環R的理想,對R中任意理想A,B,若ABP必有AP或BP,則稱P為R的素理想。它等價於對x,y∈R,若xRyP則x∈P或y∈P。當R是交換環時,P是R的素理想若且唯若對R中任意元素a,b,若ab∈P,則a∈P或b∈P。素理想在交換環的理想理論中有重要作用。若對任意環R,a,b∈R,由ab∈P得出a∈P或b∈P,則稱P為R的完全素理想。因此,對交換環來說,素與完全素概念是一致的。
相伴素理想
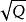 準素理想
準素理想相伴素理想(associated prime ideal)是一種特殊的素理想。包含給定準素理想的最小素理想。若Q是環R的準素理想,則Q的根 =P是包含Q的最小素理想,稱P是Q的相伴素理想,也稱屬於Q的素理想。而Q稱為P準素理想。P準素理想的交仍為P準素理想。
環
環是對並與差運算封閉的集類,測度論中重要概念之一。設F是Ω上的一個非空集類.如果它對集的並及差運算封閉,即對任何A,B∈F,都有A∪B∈F,A\B∈F,則稱F為Ω上的環。例如,若F是由實直線R上任意有限個左開右閉的有限區間的並集:
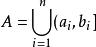 準素理想
準素理想的全體構成的集類,則F是R上的一個環。環也是對於交與對稱差運算封閉的集類,並按這兩種運算成為布爾環。要把R上的勒貝格測度和勒貝格-斯蒂爾傑斯測度以及相應的積分理論推廣到更一般的集合上,就需要做一系列奠基工作,其中之一是建立一些特殊的集類並研究其性質。環以及半環、σ環、代數、σ代數等重要集類正是為了這一目的而引入的。

