概念
孤立素理想(isolated prime ideal)是一種特殊的素理想。代數幾何中代數簇的相應概念在環中的引申。若環R的理想N有極小準素分解式:
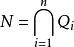 孤立素理想
孤立素理想則屬於N的素理想集Σ={P,P,…,P}(P=Q)中的極小元P稱為N的孤立素理想,而Σ中非極小元稱為N的嵌入素理想。它們所對應的Q分別稱為N的孤立準素分支和嵌入準素分支。屬於N的孤立素理想恰好是集合{P∈Spec R|PN}的全部極小元。孤立與嵌入來源於代數幾何中相應代數簇的孤立與嵌入概念。
理想
理想是集合論中的基本概念之一。設S為任意集合,若I⊆P(S)且滿足:
1.∅∈I;
2.若X,Y∈I,則X∪Y∈I;
3.若X,Y⊆S,X∈I,Y⊆X,則Y∈I;
則稱I為集合S上的理想。理想的概念在現代數學的幾乎每個分支中均有套用,且有許多變體或引申。例如,布爾代數上的理想即為集合上的理想的一種變體。設B為任意布爾代數,若B的一個子集I滿足:
1.0∈I,1∉I(其中0,1分別為布爾代數B中的零元與么元);
2.對任何u∈I,v∈I,有u+v∈I;
3.對任何u,v∈B,若u∈I且v≤u,又v∈I;
則稱I為B上的理想。
素理想
 孤立素理想
孤立素理想 孤立素理想
孤立素理想 孤立素理想
孤立素理想 孤立素理想
孤立素理想素理想是一類特殊理想。它是整數環中素數生成理想的推廣。設P是環R的理想,對R中任意理想A,B,若AB P必有A P或B P,則稱P為R的素理想。它等價於對x,y∈R,若xRy P則x∈P或y∈P。當R是交換環時,P是R的素理想若且唯若對R中任意元素a,b,若ab∈P,則a∈P或b∈P。素理想在交換環的理想理論中有重要作用。若對任意環R,a,b∈R,由ab∈P得出a∈P或b∈P,則稱P為R的完全素理想。因此,對交換環來說,素與完全素概念是一致的。
代數幾何
代數幾何是研究多項式方程組在仿射或射影空間裡的公共零點集合的幾何特性的數學分支學科。換言之,它是研究代數簇的。代數幾何與許多其他數學分支有著密切的聯繫。通常假設代數簇V中點的坐標在某個固定域k中選取,k稱為V的基域。V為不可約(即V不能分解成兩個比它小的閉代數子簇的並)時,V上所有有理函式(即兩個多項式的商)全體也構成一個域,稱為V的有理函式域,它是k的一個有限生成擴域。通過這樣的一個對應關係,代數幾何可以看成是用幾何的語言和觀點來研究有限生成擴域。
代數幾何的基本問題就是代數簇的分類。包括雙有理分類與雙正則分類(即同構分類)。若一個代數簇V到另一個代數簇V的映射誘導了函式域之間的同構,則稱該映射為雙有理映射。設有兩個代數簇V,V,若V中有一個稠密開集同構於V的一個稠密開集,則稱V,V是雙有理等價的。這等價於V和V的函式域之間的同構.按這個等價關係對代數簇進行分類就稱為雙有理分類。分類理論是這樣建立的:首先,找出代數簇的雙有理等價類;其次,在這個等價類中找到一個好對象的子集,如非奇異射影簇,對它們進行分類;第三步就是確定一個任意簇與這些好的對象相差多遠。因為任意特徵0的基域上的代數簇都雙有理等價於一個非奇異射影簇,所以為實現這三步,人們往往先找一組與非奇異射影簇對應的整數,稱為它的數值不變數.例如,在射影簇的情形,它的各階上同調空間的維數就都是數值不變數。然後試圖在所有具有相同的數值不變數的代數簇的集合上建立一個自然的代數結構,稱為它們的參量簇,使得當參量簇中的點在某個代數結構中變化時,對應的代數簇也在相應的代數結構中變化。目前,只有代數曲線、一部分代數曲面以及少數特殊的高維代數簇有較完整的分類。
20世紀初期,由於抽象代數方法的引入,抽象域上的代數幾何理論建立起來了.特別是在20世紀50年代,塞爾(Serre,J.P.)把代數簇的理論建立在層的概念上,並建立了凝聚層的上同調理論,這為格羅騰迪克(Grothendieck,A.)隨後建立概形理論奠定了基礎.概形理論的建立使代數幾何的研究進入了一個全新的階段.概形的概念是代數簇的推廣.粗淺地,它允許點的坐標在任意有單位元的交換環中選取,並允許結構層中有冪零元.概形理論把代數幾何和代數數域的算術統一到了一個共同的語言之下,這使得在代數數論的研究中可以套用代數幾何中大量的概念、方法和結果。
20世紀以來,複數域上代數幾何中的超越方法也有重大的進展,例如,德·拉姆(de Rham,G.-W.)的解析上同調理論,霍奇(Hodge,W.V.D.)的調和積分理論的套用,小平邦彥和斯潘塞(Spencer,D.C.)的變形理論以及格里菲思(Griffiths,P.)的一些重要工作。這使得代數幾何的研究可以套用偏微分方程、微分幾何、拓撲學等理論。
代數簇
代數簇是代數幾何的基本研究對象。設k是一個域,域k上的代數簇就是一個整的、分離、有限型k概形。這裡的基域k往往被取作代數閉域。若一個代數簇又是射影、擬射影、仿射或正常k概形,則把這個代數簇相應地稱為射影、擬射影、仿射、完備(代數)簇。射影簇必定是完備簇,反之則不然。
設S是一個概型,φ是概型X到S的態射,則稱X是一個S-概型,如果S=SpecR,則稱X是一個R-概型。設f是概型X到Y的態射,如果△: X→XX,x→(x,x)是閉的浸入,則稱X在Y上可分,若Y=SpecR,則稱X是可分的。態射f:X→Y稱為有限型的,如果存在Y的仿射開覆蓋{Y|λ∈∧} 使得每個X=f(Y) 可以被有限個仿射開子集覆蓋,而X=SpecB,Yλ=SpecA每個B是有限生成的A代數。若X→SpecR是有限型的,則稱X是R-代數的。設k是一個代數閉域,V是一個整的,可分的在k上代數的k-概型,則我們稱V是k上的一個代數簇。設(X,φ),(Y,φ)是S-概型,f: X→Y是態射,如果→f=φ,則稱f是S-態射。設X,Y是R-概型,令E={ (U,φ)|U是X的稠密開子集,φ:U→Y是R-態射},在E上引入等價關係 (U,φ)~ (V,φ) 若且唯若對於U∩V的某個稠密開子集W,|w=Φ|W。E/~的元素稱為有理映射,若Y=Spec[X],則稱為有理函式,X上所有有理函式的集合記作Rat(X)。若V是域k上的代數簇,則Rat(V)稱為V的函式域。設f是X到Y的有理映射,如果存在(U,φ)∈f,使得φ(U)是Y的稠密子集,則稱f是控制的。設V,W是代數簇,f:V→W是控制的有理映射,如果存在有理映射g:W→V使得g◦f是恆等映射,則稱f是雙有理映射。V到V的所有雙有理映射作成一個群,稱為V的雙有理同構群。如果有V到W的雙有理映射,則稱V與W雙有理等價。一維的代數簇稱為曲線,二維的代數簇稱為曲面。曲面S上的曲線C是曲面S的一維閉子簇。
環
環是對並與差運算封閉的集類,測度論中重要概念之一。設F是Ω上的一個非空集類。如果它對集的並及差運算封閉,即對任何A,B∈F,都有A∪B∈F,A\B∈F,則稱F為Ω上的環。例如,若F是由實直線R上任意有限個左開右閉的有限區間的並集:
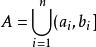 孤立素理想
孤立素理想的全體構成的集類,則F是R上的一個環.環也是對於交與對稱差運算封閉的集類,並按這兩種運算成為布爾環。要把R上的勒貝格測度和勒貝格-斯蒂爾傑斯測度以及相應的積分理論推廣到更一般的集合上,就需要做一系列奠基工作,其中之一是建立一些特殊的集類並研究其性質。環以及半環、σ環、代數、σ代數等重要集類正是為了這一目的而引入的。
