定義
正定矩陣
(1)廣義定義:設M是n階方陣,如果對任何非零向量z,都有 z Mz> 0,其中 z 表示z的轉置,就稱M為正定矩陣。
例如:B為n階矩陣,E為單位矩陣,a為正實數。在a充分大時,aE+B為正定矩陣。(B必須為對稱陣)
(2)狹義定義:一個 n階的實對稱矩陣 M是正定的的條件是若且唯若對於所有的非零實係數向量 z,都有 z Mz> 0。其中 z表示 z的轉置。
對稱正定矩陣
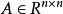 正定矩陣
正定矩陣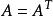 正定矩陣
正定矩陣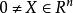 正定矩陣
正定矩陣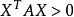 正定矩陣
正定矩陣設,若,對任意的,都有,則稱A為對稱正定矩陣。
Hermite正定矩陣
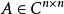 正定矩陣
正定矩陣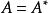 正定矩陣
正定矩陣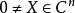 正定矩陣
正定矩陣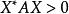 正定矩陣
正定矩陣設,若,對任意的,都有,則稱A為Hermite正定矩陣 。
性質
正定矩陣有以下性質 :
(1)正定矩陣的行列式恆為正;
(2)實對稱矩陣A正定若且唯若A與單位矩陣契約;
(3)若A是正定矩陣,則A的逆矩陣也是正定矩陣;
(4)兩個正定矩陣的和是正定矩陣;
(5)正實數與正定矩陣的乘積是正定矩陣。
等價命題
對於n階實對稱矩陣A,下列條件是等價的:
(1)A是正定矩陣;
(2)A的一切順序主子式均為正;
(3)A的一切主子式均為正;
(4)A的特徵值均為正;
(5)存在實可逆矩陣C,使A=C′C;
(6)存在秩為n的m×n實矩陣B,使A=B′B;
(7)存在主對角線元素全為正的實三角矩陣R,使A=R′R 。
充要條件
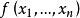 正定矩陣
正定矩陣 正定矩陣
正定矩陣(1)n 元實二次型正定它的正慣性指數為 n;
 正定矩陣
正定矩陣 正定矩陣
正定矩陣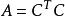 正定矩陣
正定矩陣(2) 一個實對稱矩陣 A 正定A 與 E 契約,即可逆矩陣 C,使得;
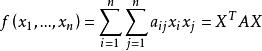 正定矩陣
正定矩陣 正定矩陣
正定矩陣(3) 實二次型是正定的A的順序主子式全大於零;
 正定矩陣
正定矩陣(4) 一個實對稱矩陣 A 正定A 的特徵值全大於零;
 正定矩陣
正定矩陣(5) 一個實對稱矩陣 A 正定A 的主子式全大於零;
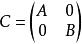 正定矩陣
正定矩陣 正定矩陣
正定矩陣(6)A ,B 是實對稱矩陣,則正定A,B均正定;
 正定矩陣
正定矩陣 正定矩陣
正定矩陣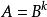 正定矩陣
正定矩陣(7)A 實對稱矩陣, A 正定正定矩陣 B,使得,(k 為任意正整數)。
判定的方法
根據正定矩陣的定義及性質,判別對稱矩陣A的正定性有兩種方法:
(1)求出A的所有特徵值。若A的特徵值均為正數,則A是正定的;若A的特徵值均為負數,則A為負定的。
(2)計算A的各階主子式。若A的各階主子式均大於零,則A是正定的;若A的各階主子式中,奇數階主子式為負,偶數階為正,則A為負定的。
套用
對於具體的實對稱矩陣,常用矩陣的各階順序主子式是否大於零來判斷其正定性;對於抽象的矩陣,由給定矩陣的正定性,利用標準型,特徵值及充分必要條件來證相關矩陣的正定性。

