定義
 正則函式
正則函式 正則函式
正則函式 正則函式
正則函式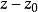 正則函式
正則函式 正則函式
正則函式 正則函式
正則函式正則函式亦稱 全純函式或 解析函式,是解析函式論的主要研究對象,對於定義於複平面上區域 內的復變數z的單值函式 ,如果它在D內的每個點 的一個鄰域內都可以用 的冪級數表示,則稱 在D內解析,外爾斯特拉斯(K.(T.W.)Weierstrass)從冪級數出發,建立了解析函式的級數理論,如果在 內的每個點z處,極限
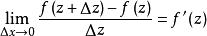 正則函式
正則函式 正則函式
正則函式 正則函式
正則函式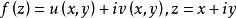 正則函式
正則函式 正則函式
正則函式 正則函式
正則函式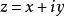 正則函式
正則函式(稱為函式 在z點的導數)都存在,柯西(A.-L.Cauchy)稱在D內是解析的,這兩個定義是等價的。函式 在D內解析的另一個等價條件是: 在 內的每一個點 處存在連續偏導數,並且滿足柯西-黎曼方程(或稱柯西-黎曼條件):
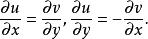 正則函式
正則函式這個條件有時簡稱C-R條件或稱 達朗貝爾-歐拉條件,函式f(z)在區域D內解析的第四個等價條件是莫雷拉定理。
性質定理
 正則函式
正則函式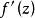 正則函式
正則函式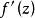 正則函式
正則函式性質1 函式 在域D內每一點具有導數 ,而且導數 在D內為連續。
 正則函式
正則函式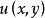 正則函式
正則函式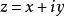 正則函式
正則函式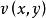 正則函式
正則函式性質2 在域D中,函式 的實部 (於此, ),)和虛部 具有一次連續偏導數
 正則函式
正則函式它們在D內滿足恆等條件
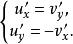 正則函式
正則函式 正則函式
正則函式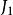 正則函式
正則函式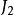 正則函式
正則函式性質3 這項性質預先假定了函式 在域D內為連續;下面,我們把它用兩種不同方式( 和 )敘述出來,這兩種方式等價。
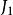 正則函式
正則函式 正則函式
正則函式 正則函式
正則函式 正則函式
正則函式 正則函式
正則函式:無論對於域D內的任何兩點 和b,沿D內從 到b所引的(有限長)曲線C所取的積分 與積分的路徑無關,而僅與函式 和始點a及終點b有關;
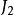 正則函式
正則函式 正則函式
正則函式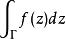 正則函式
正則函式:對於域D內的任何(有限長)閉曲線 ,沿這曲線所取的積分 等於0。
 正則函式
正則函式 正則函式
正則函式性質4 對於域D內的任何一點a,函式 在點a可展成一冪級數。詳言之:對於域D內的任何一點a,存在一列係數 (與a有關),使得級數
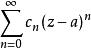 正則函式
正則函式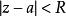 正則函式
正則函式 正則函式
正則函式在某一圓 (圓的半徑R與a有關)內收斂,且其和等於 。
 正則函式
正則函式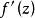 正則函式
正則函式性質5 函式 在域內每一點具有導數 。
對於與柯西同時的人黎曼(B.Riemann,1826一1866)來說(他與柯西無關地在德國奠定了複變函數論的基礎),出發點就是關係
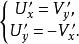 正則函式
正則函式這在後來通行叫作“柯西一黎曼條件”(或歐拉一達朗貝爾條件)。
對於比較靠近20世紀的德國學者魏爾斯特拉斯(K.Weierstrass,1855--1897)來說(他除了幾個其他的數學科目之外,並對複變函數論建立起堅實的基礎),出發點是可以展開成冪級數這種性質(性質4)。
最後,從近代的數學方法論的觀點來看,在建立複變函數論的時候,採用解析函式的積分性質(性質3)可能有很大的優越性,這是因為在很快得出柯西積分之後,就可以從它進而導出可微分性,以及可以展成冪級數性等。
