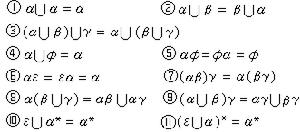詞語簡介
形式語言理論中最簡單的語言類,是上下文無關語言類的一個真子類,在喬姆斯基語言分層中處於最低層。又稱 3型語言。正則語言有兩種描述方法:①文法描述;②正則表達式與接受器。正則語言已套用於電腦程式語言編譯的詞法分析、開關電路設計等方面。
描述方法
文法描述:正則語言由正則文法(或稱右線性文法,見形式語言理論)所生成。當限制產生式形式為A→Bt或A→t時,文法為左線性文法(其中A,B是非終結符,t是終結符)。每一右線性文法必有與之等價的左線性文法存在,即是說,這兩種文法生成相同的語言。
正則表達式與接受器:正則語言是正則集,可以用稱為正則表達式的簡單式子來表示。對任意一個給定的正則表達式可以構造出不確定有限自動機來接收它,反過來,從任意有限自動機可以找出它所接受的正則表達式。
正則表達式 正則表達式描述的語言是正則集。令∑是一個有限集,遞歸地定義如下:
①φ、ε、ɑ(凬ɑ∈∑)是∑上的正則表達式,它們所表示的字集分別為空集,{ε}、{ɑ}都是正則集。②若 刅、β是∑上的正則表達式,則刅∪β、刅·β、刅*也是∑上的正則表達式,它們所表示的字集{刅}、{β}、{刅}∪{β}、{刅}{β}、{刅*}是相應的正則集(運算符∪、·、*分別為並、連線、乘冪閉包。式子裡連線符·可以略去不寫,運算的優先順序為:*,·,∪)。③只有有限次使用①、②確定出的表達式才是∑上的正則表達式,只有這些正則表達式所表示的字集才是∑上的正則集。正則集就是正則語言。
為了簡化正則表達式,常用下列等式 用①~⑥可以把正則表達式刅寫成正則表達式β,即刅與β相似。
正則表達式的導式類似於微積分學中的導式。任一正則表達式刅關於x(∈∑*)的導式Dx刅 遞歸定義如下: 每一正則表達式只有有限個不相似的導式。表中為正則表達式複雜性的兩種測度:H和N。 正則語言的性質 泵作用引理:若R是正則語言,則對R中所有字長不小於n的字w=xyz(y厵ε且xy的字長不超過n)和所有非負整數i必有xyiZ∈R。 這個引理是證明某些語言非正則的有力工具,而且有助於建立算法,以便判斷一個給定的有限自動機所接受的語言是有限還是無限的。
對語言運算的封閉性:封閉的意思是將語言運算用到正則集上,其結果仍然是正則集。這對判別某些語言的正則性是有作用的。正則語言類是對並、連線、乘冪閉包運算封閉的最小語言類,並且對於交、補、逆、商、替換、逆同態等運算也封閉。
正則語言的重要結果:與半群(服從結合律的二元運算的非空集),態射、直積等抽象代數的概念相聯繫已形成學科性的課題,已經得到的重要結果有:
① R吇∑*,R是正則語言的等價條件為:∑*關於右同餘關係ER的等價類類數有限等價關係ER規定為:x,y∈∑*,xERy若且唯若對每一Z∈∑*或者xz與yz都在R中或者都不在R中。
② R的語法么半群MR的元素個數有限(么半群是有麼元的半群,麼元類似於數 1對數的乘法所起的作用,例如∑*對連線運算構成一個半群,由於對任意x∈∑*,xε=εx=x,故空字ε就是∑*的麼元,因而∑*是一個么半群)。么半群∑*到PF(Q)的態射f下的象MR就是R的語法么半群,其中PF(Q)是Q到Q的全體偏函式(即對Q的元不一定都有定義的函式)對函式合成運算構成的么半群,Q是接受語言R的自動機M的狀態集合,態射f的定義為f:x→嗞x,式中δ是M的狀態轉移函式。
③ 對每一正則語言R都存在同態映射h1、h2、h3、h4使上的語言。
④ 正則語言的星流形與有限么半群流形之間有一一映射存在,這是塞繆爾·愛倫堡定理。若干正則語言形成的族在布爾運算、派生、逆同態下封閉時就是一個星流形。若干有限么半群形成的族在態射象、子么半群、有限直積下封閉時就是一個么半群流形。
參考書目
M. A. Arbib,Theories of Abstract Automata,PrenticeHall, Englewood Cliffs, N. J., 1969