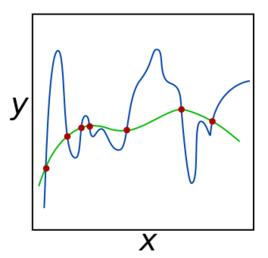
定義
正則化:代數幾何中的一個概念。
通俗定義
就是給平面不可約代數曲線以某種形式的全純參數表示。
即對於PC^2中的不可約代數曲線C,尋找一個緊Riemann面C*和一個全純映射σ:C*→PC^2,使得σ(C*)=C
嚴格定義
設C是不可約平面代數曲線,S是C的奇點的集合。如果存在緊Riemann面C*及全純映射σ:C*→PC^2,使得
(1) σ(C*)=C (2) σ^(-1)(S)是有限點集 (3) σ:C*\σ^(-1)(S)→C\S是一對一的映射
則稱(C*,σ)為C的正則化。不至於混淆的時候,也可以稱C*為C的正則化。
正則化的做法,實際上是在不可約平面代數曲線的奇點處,把具有不同切線的曲線分支分開,從而消除這種奇異性。
主要解決的問題
正則化就是對最小化經驗誤差函式上加約束,這樣的約束可以解釋為先驗知識(正則化參數等價於對參數引入先驗分布)。約束有引導作用,在最佳化誤差函式的時候傾向於選擇滿足約束的梯度減少的方向,使最終的解傾向於符合先驗知識(如一般的l-norm先驗,表示原問題更可能是比較簡單的,這樣的最佳化傾向於產生參數值量級小的解,一般對應於稀疏參數的平滑解)。
同時,正則化解決了逆問題的不適定性,產生的解是存在,唯一同時也依賴於數據的,噪聲對不適定的影響就弱,解就不會過擬合,而且如果先驗(正則化)合適,則解就傾向於是符合真解(更不會過擬合了),即使訓練集中彼此間不相關的樣本數很少。
1.正則化就是對最小化經驗誤差函式上加約束,這樣的約束可以解釋為先驗知識(正則化參數等價於對參數引入先驗分布)。約束有引導作用,在最佳化誤差函式的時候傾向於選擇滿足約束的梯度減少的方向,使最終的解傾向於符合先驗知識(如一般的l-norm先驗,表示原問題更可能是比較簡單的,這樣的最佳化傾向於產生參數值量級小的解,一般對應於稀疏參數的平滑解)。
2.同時,正則化解決了逆問題的不適定性,產生的解是存在,唯一同時也依賴於數據的,噪聲對不適定的影響就弱,解就不會過擬合,而且如果先驗(正則化)合適,則解就傾向於是符合真解(更不會過擬合了),即使訓練集中彼此間不相關的樣本數很少。
形式
反問題有兩種形式。最普遍的形式是已知系統和輸出求輸入,另一種系統未知的情況通常也被視為反問題。許多反問題很難被解決,但是其他反問題卻很容易得到答案。顯然,易於解決的問題不會比很難解決的問題更能引起人們的興趣,我們直接解決它們就可以了。那些很難被解決的問題則被稱為不適定的。一個不適定問題通常是病態的,並且不論是簡單地還是複雜地改變問題本身的形式都不會顯著地改善病態問題。另一方面,病態問題不一定是不適定的,因為通過改變問題的形式往往可以改善病態問題。在嚴格的數學意義上,我們通常不可能對不適定問題進行求解並得到準確解答。然而,通過使用我們的先驗知識,我們通常有希望能夠得到一個接近準確解答的答案。
用途
求解不適定問題的普遍方法是:用一組與原不適定問題相“鄰近”的適定問題的解去逼近原問題的解,這種方法稱為正則化方法。如何建立有效的正則化方法是反問題領域中不適定問題研究的重要內容。通常的正則化方法有基於變分原理的Tikhonov 正則化、各種疊代方法以及其它的一些改進方法,這些方法都是求解不適定問題的有效方法,在各類反問題的研究中被廣泛採用,並得到深入研究。
訓練方法
梯度下降法
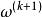 正則化
正則化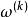 正則化
正則化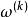 正則化
正則化=−α∇J()
係數w的更新公式為:
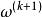 正則化
正則化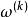 正則化
正則化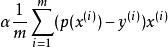 正則化
正則化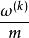 正則化
正則化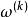 正則化
正則化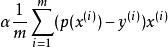 正則化
正則化= − −λ = (1−λ/m)−
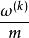 正則化
正則化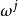 正則化
正則化可見,正則化後的疊代算法和沒有正則化的疊代形式非常像,唯一的差別在與每次疊代都要多減去一個λ 。相當於如果當前 已經比較大了,那么,w要先多減去一點,然按梯度方向進行疊代。
另外,上式的正則化項與m成反比,也就是說,樣本數越大,過擬合的問題越小,正則化的作用越弱。
牛頓法
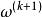 正則化
正則化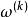 正則化
正則化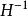 正則化
正則化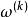 正則化
正則化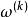 正則化
正則化=−()∇J()
引入l2-norm正則項後,一階導數和Hessian矩陣如下所示:
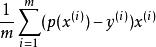 正則化
正則化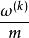 正則化
正則化∇J=−λ
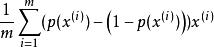 正則化
正則化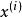 正則化
正則化 正則化
正則化 正則化
正則化H=()+λ/m
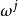 正則化
正則化與梯度下降法類似,正則化在牛頓法中也是起到懲罰大的的作用。另外,由於加了正則化項,原來不可逆的Hessian矩陣也變的可逆了。