定義
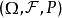 正則條件機率
正則條件機率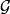 正則條件機率
正則條件機率 正則條件機率
正則條件機率 正則條件機率
正則條件機率設為機率空間,為的子代數。由條件期望的性質知:
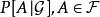 正則條件機率
正則條件機率具有以下性質:
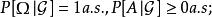 正則條件機率
正則條件機率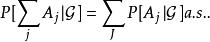 正則條件機率
正則條件機率這些性質與機率測度的性質(全空間的測度等於1,非負性,可數可加性)很相似,不同之處在於出現了例外集.
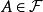 正則條件機率
正則條件機率 正則條件機率
正則條件機率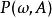 正則條件機率
正則條件機率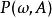 正則條件機率
正則條件機率 正則條件機率
正則條件機率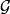 正則條件機率
正則條件機率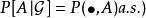 正則條件機率
正則條件機率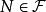 正則條件機率
正則條件機率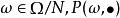 正則條件機率
正則條件機率 正則條件機率
正則條件機率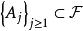 正則條件機率
正則條件機率假定對於每一個集合,我們取定的一個版本(即為上的一個確定的可測函式,並且.我們希望去掉一個例外集(機率為零)使得,對於任意的為上的一個機率測度:非負性及在全空間上的值等於1不成問題,只需要它滿足可數可加性:即對於任意可數個兩兩不相交的集合,必須有下式成立
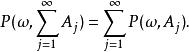 正則條件機率
正則條件機率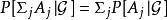 正則條件機率
正則條件機率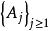 正則條件機率
正則條件機率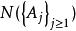 正則條件機率
正則條件機率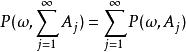 正則條件機率
正則條件機率 正則條件機率
正則條件機率 正則條件機率
正則條件機率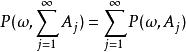 正則條件機率
正則條件機率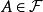 正則條件機率
正則條件機率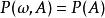 正則條件機率
正則條件機率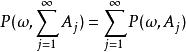 正則條件機率
正則條件機率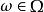 正則條件機率
正則條件機率但是,根據條件期望的定義,我們只知道。因此,對於每一個集合序列,需要去掉一個例外集才能使得式成立;而這樣的序列個數通常都是不可數的,我們知道不可數個零概集的並集不一定還是零概集(其實並起來的集合是否屬於代數我們都不知道,即並起來的集合的可測性我們一般都不知道).如果能夠去掉一個公共的零概集N,使得式成立,可在N上,對於任意集合,定義,則式對所有成立。
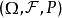 正則條件機率
正則條件機率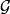 正則條件機率
正則條件機率 正則條件機率
正則條件機率 正則條件機率
正則條件機率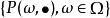 正則條件機率
正則條件機率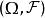 正則條件機率
正則條件機率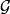 正則條件機率
正則條件機率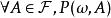 正則條件機率
正則條件機率 正則條件機率
正則條件機率設為一機率空間,為的子代數.令為上的一族機率測度,稱它為P關於的 正則條件機率,如果為的一個版本,即以下兩個條件成立:
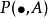 正則條件機率
正則條件機率 正則條件機率
正則條件機率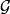 正則條件機率
正則條件機率(1)為上的可測函式;
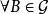 正則條件機率
正則條件機率(2),
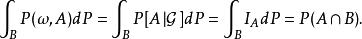 正則條件機率
正則條件機率相關定理
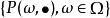 正則條件機率
正則條件機率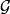 正則條件機率
正則條件機率 正則條件機率
正則條件機率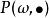 正則條件機率
正則條件機率定理1:設為P關於的正則條件機率。設X為一隨機變數,其期望存在,則對幾乎所有,X關於機率測度的積分存在,並且有
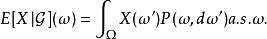 正則條件機率
正則條件機率證明 :從示性可測函式過渡到非負可測函式,再到一般可測函式(隨機變數) 。
該定理表明,有了正則條件機率,條件期望可以看做是關於條件機率的積分。
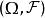 正則條件機率
正則條件機率 正則條件機率
正則條件機率 正則條件機率
正則條件機率 正則條件機率
正則條件機率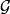 正則條件機率
正則條件機率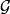 正則條件機率
正則條件機率定理2: 設為一可分可測空問,P為上的一緊機率測度,則對的任一子代數,存在P關於的正則條件機率。
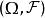 正則條件機率
正則條件機率 正則條件機率
正則條件機率 正則條件機率
正則條件機率 正則條件機率
正則條件機率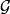 正則條件機率
正則條件機率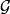 正則條件機率
正則條件機率定理3:設為一Radon可測空間,P為上的一機率測度,則對的任一子代數,存在P關於的正則條件機率。
