正則廣義函式

正則廣義函式可以看做局部可積的普通函式的廣義函式。廣義函式空間K'中那些由局部可積的普通函式f產生的廣義函式Tf稱為正則廣義函式。

簡介

正則廣義函式可以看做局部可積的普通函式的廣義函式。

廣義函式

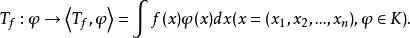正則廣義函式

設f是n維歐幾里得空間R 上的可測函式，如果對任何有界可測集M，f在M上勒貝格可積，則稱f是局部可積函式，用L表示R 上的局部可積函式全體，並將幾乎處處相等的函式視為同一函式。這樣，對每個f∈L，可以定義K上的連續泛函（即K上廣義函式）稱T為相應於f的K上的廣義函式。

定義

映射f→T是單射，如果把f就直接視為T，常稱f是K上的正則廣義函式。

換言之，廣義函式空間K'中那些由局部可積的普通函式f產生的廣義函式T稱為正則廣義函式。

類似地，在其他基本函式空間上也可引入正則廣義函式。

廣義函式空間K'

廣義函式空間K'是基本函式空間上連續線性泛函的全體。

基本函式空間K上連續線性泛函的全體稱為廣義函式空間K'（或記為'）。

按通常線性運算，K'是一線性空間，由於K'是K的共軛空間，所以在K'中可以引入弱∗拓撲。