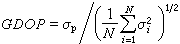定義
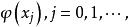 正交多項式
正交多項式對於定義在區間上[a,b]的一個函式系{ },如果其中任何兩個函式在此區間上的積分為零,而他們之中每個函式自乘的積分不等於零,
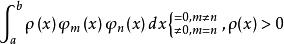 正交多項式
正交多項式即
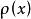 正交多項式
正交多項式則稱此函式係為在此區間上關於權函式 的正交函式系。
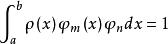 正交多項式
正交多項式當 時稱之為規範的正交函式系;當此函式系中每一個函式均為多項式時稱之為正交多項式(系)。
介紹
正交多項式最簡單的例子是勒讓德多項式,此外還有雅可比多項式、切比雪夫多項式、拉蓋爾多項式、埃爾米特多項式等,它們在微分方程、函式逼近等研究中都是極有用的工具。
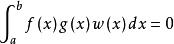 正交多項式
正交多項式設ω(x)是定義在區間【α,b】上的非負可積函式,如果它滿足條件,則稱 ω(x)為一個權函式。如果定義在[α,b]上的函式 ƒ(x)與g(x)滿足等式 ,則稱它們在【α,b】上關於權ω(x)是正交的,並稱【α,b】為它們的正交區間。對於給定的區間 【α,b】及其上的權函式ω(x),從冪函式序列出發,可以構造一列多項式: (1)
使得pn(x)的次數是n,而且其中任意兩個多項式在[α,b]上都關於ω(x)正交,這時稱 (1)為在[α,b]上關於權ω(x)的正交多項式系,並稱(1)中每一個多項式為正交多項式。如果正交多項式系(1)還滿足條件·,則稱(1)為在 【α,b】上關於權ω(x)的規範正交多項式系。
為了構造(1),先計算積分,然後記Δ -1=1
以及
則就是在[α,b]上關於權ω(x)的一個正交多項式系。常記
則n(x)的首項係數為1,n(x)的首項係數是正的,而且{n(x)}是在【α,b】上關於權ω(x)的規範正交多項式系。對於同一權函式的正交多項式系雖然很多,但是首項係數為 1的正交多項式系或首項係數為正的規範正交多項式系卻是由權ω(x)所惟一確定的。任一n次多項式都可表示為p0(x),p1(x),…,pn(x)的線性組合。pn(x)的零點全部位於(α,b)中,而且pn+1(x)的相鄰兩個零點間都有pn(x)的一個零點。此外,對於n=0,1,…都有如下的遞推公式: (2)
式中
假設函式ƒ(x)在[α,b]上關於ω(x)平方可積, 即,則稱為ƒ關於的傅立葉係數,為ƒ的傅立葉級數。若記這個級數前n+1項之和為Sn(ƒ,x),則對任何次數小於n的多項式q(x)有而且當n→∞時,這個不等式左邊所表示的偏差收斂於零。對於任何正交多項式系,都有連續函式使其傅立葉級數不一致收斂。為了研究傅立葉級數的收斂性,常記 稱為核。顯然。關於核Kn(x,t)有如下的克里斯托費爾-達布公式
由此易證:若在點x處有界,而且函式關於權ω(t)平方可積,則Sn(ƒ,x)收斂於ƒ(x)。
常用的正交多項式是關於正交的雅可比多項式
式中α>-1,β>-1,是給定的實數,對於,有
可以算出,此時遞推公式(2)中的 α=β的情況比較簡單,稱作超球多項式。當α=β=0,也即關於權時,相應的正交多項式稱作勒讓德多項式,它還可表成 當,也即關於權相應的正交多項式稱作切比雪夫多項式,它有表達式
當,也即關於權,相應的正交多項式稱作第二類切比雪夫多項式,它有表達式
這些正交多項式的正交區間都是[-1,1]。它們不僅本身有廣泛的套用,而且其零點還常作為插值過程的結點。此外,還是二階線性齊次微分方程 的解。
如果討論的是無限區間【0,+∞),則常考慮以或為權的正交多項式系與,它們依次稱作拉蓋爾多項式與埃爾米特多項式,其表達式是
遞推公式是 Ln(x)與Hn(x)
還依次滿足微分方程
常用的正交多項式
1、勒讓德多項式
2、切比雪夫多項式
3、拉蓋爾多項式
4、埃爾米特多項式
套用
用正交多項式作最小二乘曲線擬合;
套用在最佳平方逼近中;
正交回歸(正交多項式回歸)多項式回歸用作一種有效的統計方法
推廣形式
上述理論完全可能推廣為如下形式:設ψ(x)是區間【α,b】上的非減函式,。如果定義在【α,b】上的函式ƒ(x)與g(x)滿足等式,則稱他們在[α,b]上關於權 ψ(x)正交。這裡的積分是勒貝格-斯蒂爾傑斯意義下的積分。為區別上述情況,人們稱這時的權函式 ψ(x)為積分權,而將前面的權函式ω(x)稱作微分權。由積分權出發建立的正交多項式理論自然要廣泛一些。此外,還可建立多元的正交多項式理論。