正交多項式
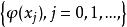 正交多項式回歸
正交多項式回歸對於定義在區間上[a,b]的一個函式系 ,如果其中任何兩個函式在此區間上的積分為零,而他們之中每個函式自乘的積分不等於零,即
 正交多項式回歸
正交多項式回歸 正交多項式回歸
正交多項式回歸則稱此函式係為在此區間上關於權函式 的正交函式系。
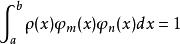 正交多項式回歸
正交多項式回歸當 時稱之為規範的正交函式系;當此函式系中每一個函式均為多項式時稱之為正交多項式(系)。
數學模型
設變數y和x的n組觀測數據服從以下k次多項式
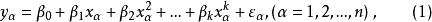 正交多項式回歸
正交多項式回歸令
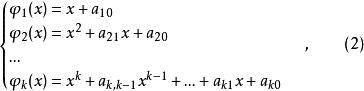 正交多項式回歸
正交多項式回歸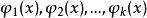 正交多項式回歸
正交多項式回歸 正交多項式回歸
正交多項式回歸分別是x的一次,二次,...,k次多項式, 是一些適當選擇的常數,如何選擇將在下面討論(i=1,2,…,n)。將(2)式帶入(1)式,則有
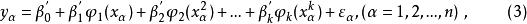 正交多項式回歸
正交多項式回歸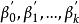 正交多項式回歸
正交多項式回歸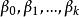 正交多項式回歸
正交多項式回歸比較(3)和(1)式可知,二者係數間存在簡單的函式關係,只要求出 ,就可以求出 。
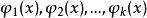 正交多項式回歸
正交多項式回歸若把 看作新的自變數,則(3)式就成為一個k元線性模型,其結構矩陣為
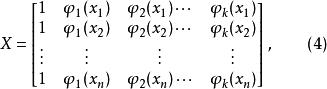 正交多項式回歸
正交多項式回歸正規方程為
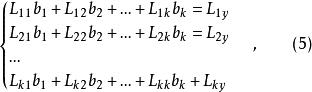 正交多項式回歸
正交多項式回歸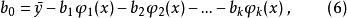 正交多項式回歸
正交多項式回歸其中
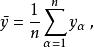 正交多項式回歸
正交多項式回歸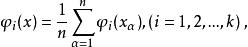 正交多項式回歸
正交多項式回歸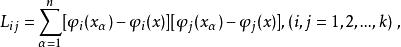 正交多項式回歸
正交多項式回歸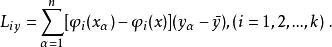 正交多項式回歸
正交多項式回歸在多項式回歸中遇到的困難是解正規方程係數矩陣的工作量太大,可以使其對角線上的元素不為零,而其餘元素均為零,從而簡化計算,而且同時消去了係數間的相關性。
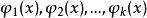 正交多項式回歸
正交多項式回歸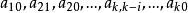 正交多項式回歸
正交多項式回歸對於 我們可以通過選擇係數 使得
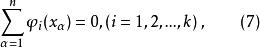 正交多項式回歸
正交多項式回歸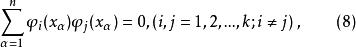 正交多項式回歸
正交多項式回歸從而使
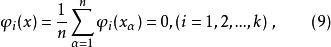 正交多項式回歸
正交多項式回歸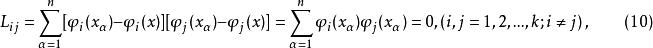 正交多項式回歸
正交多項式回歸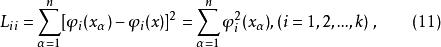 正交多項式回歸
正交多項式回歸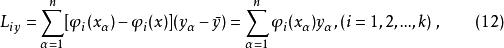 正交多項式回歸
正交多項式回歸則正規方程組為
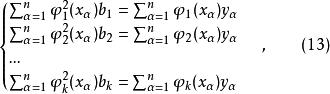 正交多項式回歸
正交多項式回歸回歸係數為
 正交多項式回歸
正交多項式回歸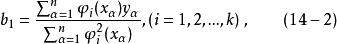 正交多項式回歸
正交多項式回歸滿足(7)和(8)式的多項式組…我們稱之為 正交多項式。
在正交多項式回歸中自變數的選擇是等間隔的,設間隔為h,x=a, 則
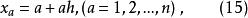 正交多項式回歸
正交多項式回歸若令
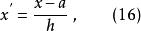 正交多項式回歸
正交多項式回歸則
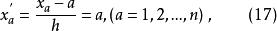 正交多項式回歸
正交多項式回歸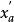 正交多項式回歸
正交多項式回歸是1至n的正整數。
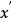 正交多項式回歸
正交多項式回歸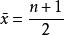 正交多項式回歸
正交多項式回歸為簡化問題,用 代替x作為自變數。在條件許可時,取自變數x=1,x=2,…,x=n。當x=1,x=2,…,x=n時有 ,這時驗證以下多項式是正交的,即
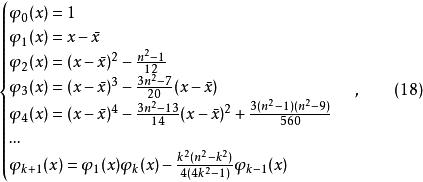 正交多項式回歸
正交多項式回歸 正交多項式回歸
正交多項式回歸顯然,當x取正整數時, 不一定是整數,為了克服這給計算上帶來的困難,取
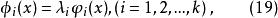 正交多項式回歸
正交多項式回歸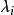 正交多項式回歸
正交多項式回歸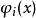 正交多項式回歸
正交多項式回歸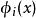 正交多項式回歸
正交多項式回歸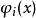 正交多項式回歸
正交多項式回歸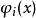 正交多項式回歸
正交多項式回歸使x取正整數時 是整數。可以驗證用正交多項式 代替 所求得的回歸方程與用正交多項式 所求得的回歸方程是完全一樣的。
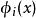 正交多項式回歸
正交多項式回歸對於正交多項式 有
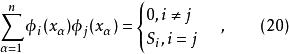 正交多項式回歸
正交多項式回歸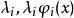 正交多項式回歸
正交多項式回歸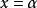 正交多項式回歸
正交多項式回歸不同的n相對應的 在 時的值以及S值都已製成正交多項式表,根據正交多項式表,可以計算出回歸方程的係數。令
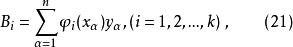 正交多項式回歸
正交多項式回歸則
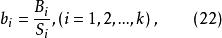 正交多項式回歸
正交多項式回歸回歸方程為
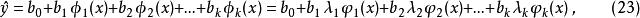 正交多項式回歸
正交多項式回歸由於正交多項式回歸係數之間不存在相關性,因此某一項如果不顯著,只要將它剔除即可,而不必對整個回歸方程重新計算。
回歸係數的顯著性檢驗
正交多項式回歸方程與回歸係數的顯著性檢驗可利用正交多項式的性質按表1進行。經檢驗不顯著的高次項可以剔除,將其效應併入殘差平方和,自由度也同時併入,如果對回歸方程精度不滿意,可以增加高次項,而已經計算出的結果不必重算。
表1 正交多項式回歸方差分析表
| 方差來源 | 平方和 | 自由度 | 均方 | F | 顯著性 |
| 回歸 | 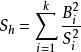 正交多項式回歸 正交多項式回歸 | k | 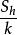 正交多項式回歸 正交多項式回歸 | 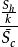 正交多項式回歸 正交多項式回歸 | |
一次項 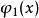 正交多項式回歸 正交多項式回歸 | 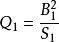 正交多項式回歸 正交多項式回歸 | 1 | 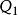 正交多項式回歸 正交多項式回歸 | 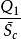 正交多項式回歸 正交多項式回歸 | |
二次項 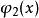 正交多項式回歸 正交多項式回歸 | 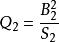 正交多項式回歸 正交多項式回歸 | 1 | 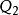 正交多項式回歸 正交多項式回歸 | 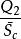 正交多項式回歸 正交多項式回歸 | |
| ... | ... | ... | ... | ... | ... |
k次項 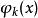 正交多項式回歸 正交多項式回歸 | 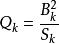 正交多項式回歸 正交多項式回歸 | 1 | 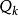 正交多項式回歸 正交多項式回歸 | 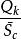 正交多項式回歸 正交多項式回歸 | |
| 殘差 | 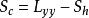 正交多項式回歸 正交多項式回歸 | n-k-1 | 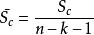 正交多項式回歸 正交多項式回歸 | ||
| 總計 | 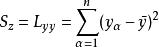 正交多項式回歸 正交多項式回歸 | n-1 |
程式框圖
1.數學模型:
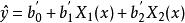 正交多項式回歸
正交多項式回歸2.變數及數組說明:
J-正確讀入數據的控制變數;
N-試驗組數;
M-所取正交多項式項數;
X(I)-存自變數數值;
Y(I)-存因變數數值;
Z(I)-存Y(I)的平方項;
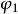 正交多項式回歸
正交多項式回歸E(I,1)-存在正交多項式一次項 ;
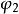 正交多項式回歸
正交多項式回歸E(I,2)-存在正交多項式二次項 ;
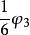 正交多項式回歸
正交多項式回歸E(I,3)-存在正交多項式三次項 (其中I=1,…N);
S(J)-結構矩陣逆矩陣元素 J=1,2,3;
B(J)-常數項矩陣B J=1,2,3;
D(J)-回歸係數 J=0,1,2,3;
Q(J)-偏回歸平方和 J=0,1,2,3;
S-剩餘平方和;
S-標準離差;
S-總平方和;
F(J)-F檢驗值。
3.程式框圖:
見如下圖1
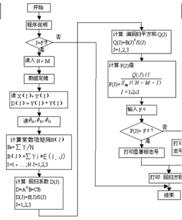 圖1
圖1