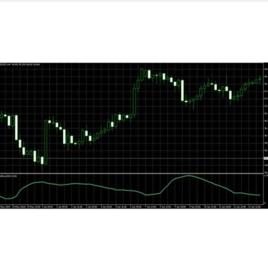
定義
多數翻譯為標準差,偶爾翻譯為標準離差、標準偏差,也稱均方差(mean square error)。各數據偏離平均數的距離(離均差)的平均數,它是離均差平方和平均後的方根。用σ表示。因此,標準差也是一種平均數 ; 標準離差表示數據的離散程度。
外匯術語:標準離差指統計上用於衡量一組數值中某一數值與其平均值差異程度的指標。標準離差被用來評估價格可能的變化或波動程度。標準離差越大,價格波動的範圍就越廣,股票等金融工具表現的波動就越大。
方差
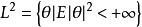 標準離差
標準離差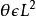 標準離差
標準離差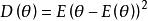 標準離差
標準離差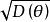 標準離差
標準離差描述隨機變數取值相對於其均值分散程度的數字特徵。以 表示平方可積隨機變數全體,對任意 ,稱 為θ(及其機率分布)的方差。方差的算術平方根 稱為標準離差。 標準離差能反映一個數據集的離散程度。平均數相同的,標準離差未必相同。
例如,A、B兩組各有6位學生參加同一次語文測驗,A組的分數為95、85、75、65、55、45,B組的分數為73、72、71、69、68、67。這兩組的平均數都是70,但A組的標準差為17.08分,B組的標準差為2.16分,說明A組學生之間的差距要比B組學生之間的差距大得多。
標準差也被稱為實驗標準差。關於這個函式在EXCEL中的STDEVP函式有詳細描述,EXCEL中文版里使用的就是“標準偏差”字樣。但我國的中文教材等通常還是使用的是“標準差”。
標準離差與標準誤差
標準離差表示樣本數據的離散程度。標準離差就是樣本平均數方差的開平方,標準離差通常是相對於樣本數據的平均值而定的,通常用M±SD來表示,表示樣本某個數據觀察值相距平均值有多遠。從這裡可以看到,標準離差受到極值的影響。標準離差越小,表明數據越聚集;標準離差越大,表明數據越離散。標準離差的大小因測驗而定,如果一個測驗是學術測驗,標準離差大,表示學生分數的離散程度大,更能夠測量出學生的學業水平;如果一個測驗測量的是某種心理品質,標準離差小,表明所編寫的題目是同質的,這時候的標準離差小的更好。標準離差與常態分配有密切聯繫:在常態分配中,1個標準差等於常態分配下曲線的68.26%的面積,1.96個標準差等於95%的面積。這在測驗分數等值上有重要作用。
標準誤差表示抽樣的誤差。因為從一個總體中可以抽取出無數多種樣本,每一個樣本的數據都是對總體的數據的估計。標準誤差代表的就是當前的樣本對總體數據的估計,標準誤差代表的就是樣本均數與總體均數的相對誤差。標準誤差是由樣本的標準差除以樣本容量的開平方來計算的。從這裡可以看到,標準誤差更大的是受到樣本容量的影響。樣本容量越大,標準誤差越小,那么抽樣誤差就越小,就表明所抽取的樣本能夠較好地代表總體。
一個常態分配的總體,抽取n個作為樣本,可以得到樣本平均值,用樣本均值估計總體均值需要考慮樣本均值的方差或標準離差(也就是標準誤差)。
樣本標準差
在真實世界中,除非在某些特殊情況下,不然找到一個總體的真實的標準差是不現實的。大多數情況下,總體標準差是通過隨機抽取一定量的樣本並計算樣本標準差估計的。
技術指標命名為標準離差(StdDev)是由於市場的波動因素。這個指標的特性是價格變動比率與移動平均數有關。因此,如果指標價值很大,市場的波動性和柱價格的分散都會涉及到移動平均數。如果指標價值不大,就意味著市場波動性低並且柱價格是和移動平均數相近的。通常來講,這個指標被作為其他指標的一個組成部分套用。因此,當保力加通道指標被計算時,商品的標準離差價值被添加到其移動平均數上。積極交易活動和遲緩市場的行為表現為相互替換。這樣,指標可以很輕鬆地詮釋:如果指標價值過低,市場是完全不活躍的,指標可以使其期待下一個巔峰;相反地,如果其價值過高,它很有可能過於活躍的交易將會帶來虧損。
標準離差是以絕對數來衡量待決策方案的風險,在期望值相同的情況下,標準離差越大,風險越大;相反,標準離差越小,風險越小。標準離差的局限性在於它是一個絕對數,適用於期望值相同決策方案時風險程度的比較;標準離差是反映機率分布中各種可能結果對期望值的偏離程度的一個數值。其中機率是指隨機事件發生的可能性。機率分布是指一項活動可能出現的所有結果的機率的集合。機率分布有兩種類型:不連續的機率分布;連續的機率分布。標準離差是以價格與其移動平均線的差的平方根來計算的。
標準差與標準誤都是數理統計學的內容,兩者不但在字面上比較相近,而且兩者都是表示距離某一個標準值或中間值的離散程度,即都表示變異程度,但是兩者是有著較大的區別的。
首先要從統計抽樣的方面說起。現實生活或者調查研究中,我們常常無法對某類欲進行調查的目標群體的所有成員都加以施測,而只能夠在所有成員(即樣本)中抽取一些成員出來進行調查,然後利用統計原理和方法對所得數據進行分析,分析出來的數據結果就是樣本的結果,然後用樣本結果推斷總體的情況。一個總體可以抽取出多個樣本,所抽取的樣本越多,其樣本均值就越接近總體數據的平均值。
套用
簡單來說,標準離差是一組數值自平均值分散開來的程度的一種測量觀念。一個較大的標準差,代表大部分的數值和其平均值之間差異較大;一個較小的標準離差,代表這些數值較接近平均值。例如,兩組數的集合 {0, 5, 9, 14} 和 {5, 6, 8, 9} 其平均值都是 7 ,但第二個集合具有較小的標準離差。
物理
標準離差可以當作不確定性的一種測量。在物理科學中,做重複性測量時,測量數值集合的標準離差代表這些測量的精確度。當要決定測量值是否符合預測值,測量值的標準差占有決定性重要角色:如果測量平均值與預測值相差太遠(同時與標準差數值做比較),則認為測量值與預測值互相矛盾。這很容易理解,因為如果測量值都落在一定數值範圍之外,可以合理推論預測值是否正確。
選基金
標準差套用於投資上,可作為量度回報穩定性的指標。標準差數值越大,代表回報遠離過去平均數值,回報較不穩定故風險越高。相反,標準差數值越小,代表回報較為穩定,風險亦較小。
基金的算法
近期業績表現最佳的基金之後,基金表現反而不如預期,這是因為所選基金波動度太大,沒有穩定的表現。
衡量基金波動程度的工具就是標準差(Standard Deviation)。標準差是指基金可能的變動程度。標準差越大,基金未來淨值可能變動的程度就越大,穩定度就越小,風險就越高。
比方說,一年期標準差是30%的基金,表示這類基金的淨值在一年內可能上漲30%,但也可能下跌30%。因此,如果有兩隻收益率相同的基金,投資人應該選擇標準離差較小的基金(承受較小的風險得到相同的收益),如果有兩隻相同標準離差的基金,則應該選擇收益較高的基金(承受相同的風險,但是收益更高)。建議投資人同時將收益和風險計入,以此來判斷基金。例如,A基金二年期的收益率為36%,標準差為18%;B基金二年期收益率為24%,標準離差為8%,從數據上看,A基金的收益高於B基金,但同時風險也大於B基金。A基金的“每單位風險收益率”為2(0.36/0.18),而B基金為3(0.24/0.08)。因此,原先僅僅以收益評價是A基金較優,但是經過標準離差即風險因素調整後,B基金反而更為優異。
另外,標準離差也可以用來判斷基金屬性。例如股票基金的平均標準離差為5.14,積極型基金的平均標準離差為5.04;保守配置型基金的平均標準離差為4.86;普通債券基金平均標準離差為2.91;貨幣基金平均標準離差則為0.19;由此可見,越是積極型的基金,標準離差越大;而如果投資人持有的基金標準離差高於平均值,則表示風險較高。
股市分析中
股票價格的波動是股票市場風險的表現,因此股票市場風險分析就是對股票市場價格波動進行分析。波動性代表了未來價格取值的不確定性,這種不確定性一般用方差或標準離差來刻畫(Markowitz,1952)。通過標準離差比較可以看出上證波動率變異係數與標準普爾波動率變異係數的關係,以此判斷中國股市長期穩定性。